多元函数微分

我的数学专升本笔记

一，计算多元微分表达式的方法：

能凑则凑，不能凑用换元

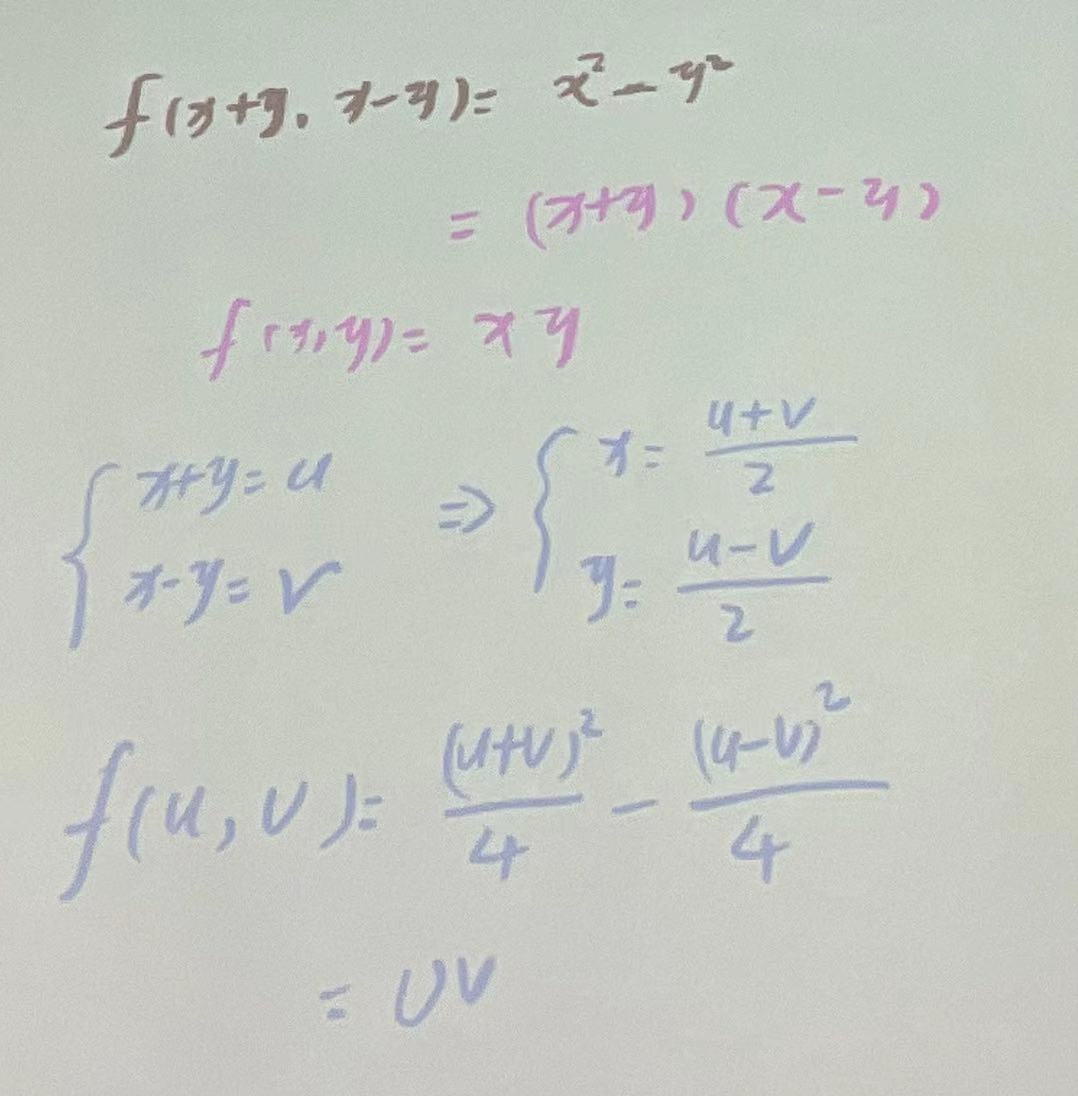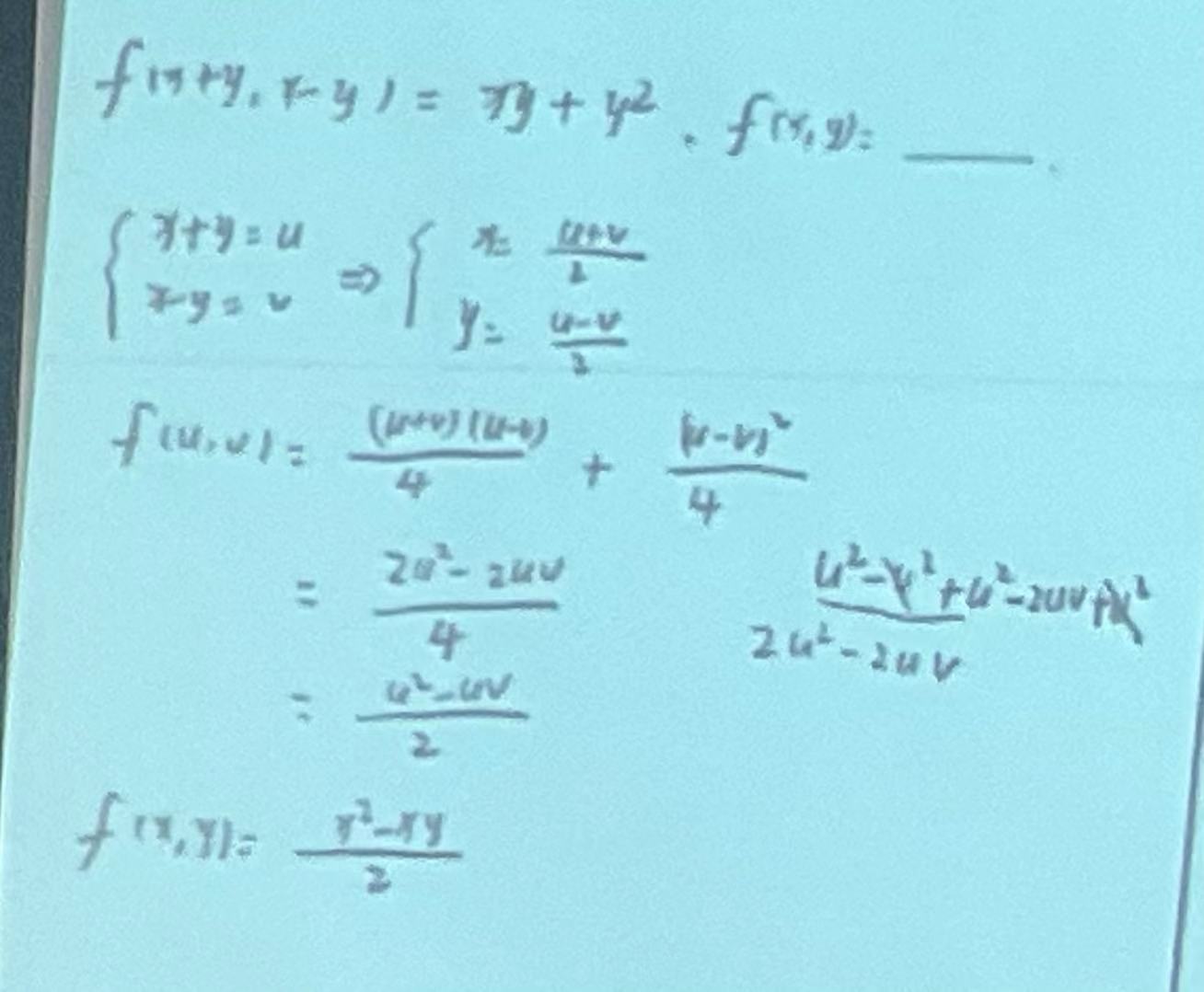二，（代数运算）计算多元极限的方法：

1. 能代入，代入即是极限值；
2. 化简之后能代入，代入也是极限值；
3. 否则，转换为一元求极限；

二，偏导

偏导数的求法：

1. 对谁求偏导谁是变量，其它当作常数，求偏导数再代入；
2. 对谁求偏导数，将其它量代入，转化为一元函数求导，再代入；
3. 分段函数在分段点处，利用偏导定义求偏导；

性质：

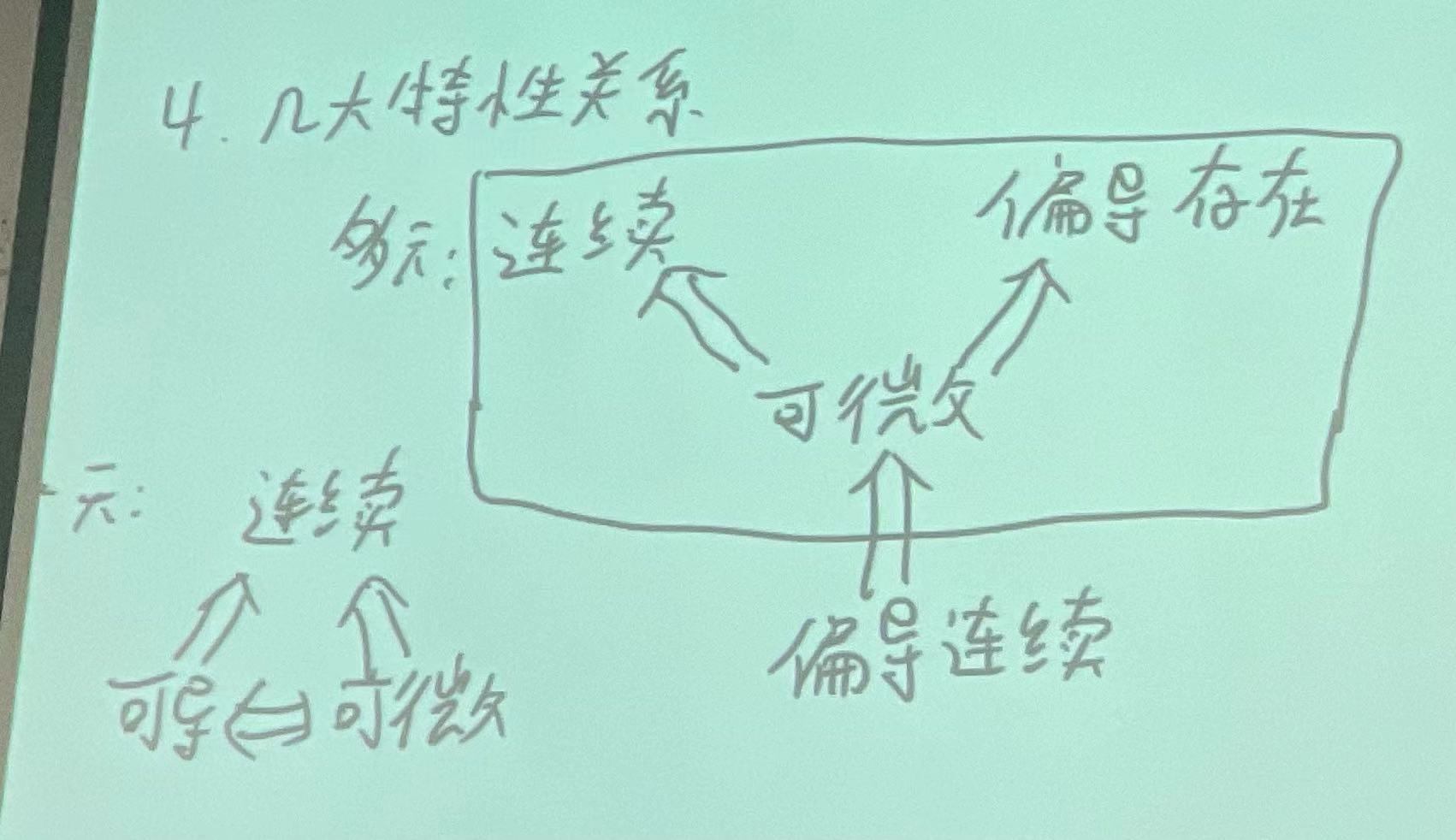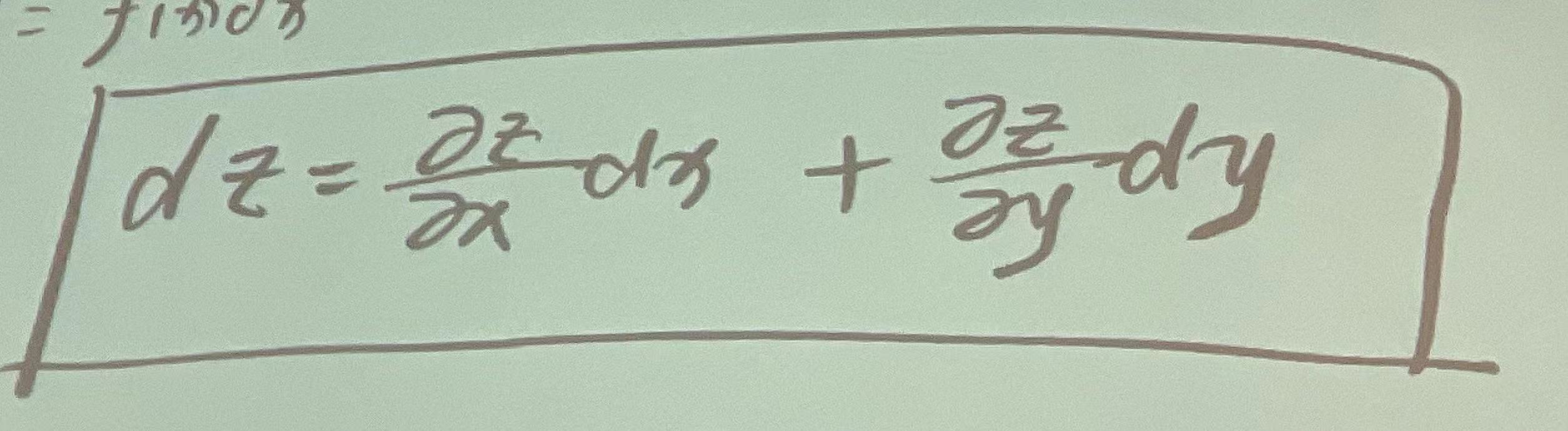全微分，显函数求偏导，隐函数求偏导

复合函数求偏导：

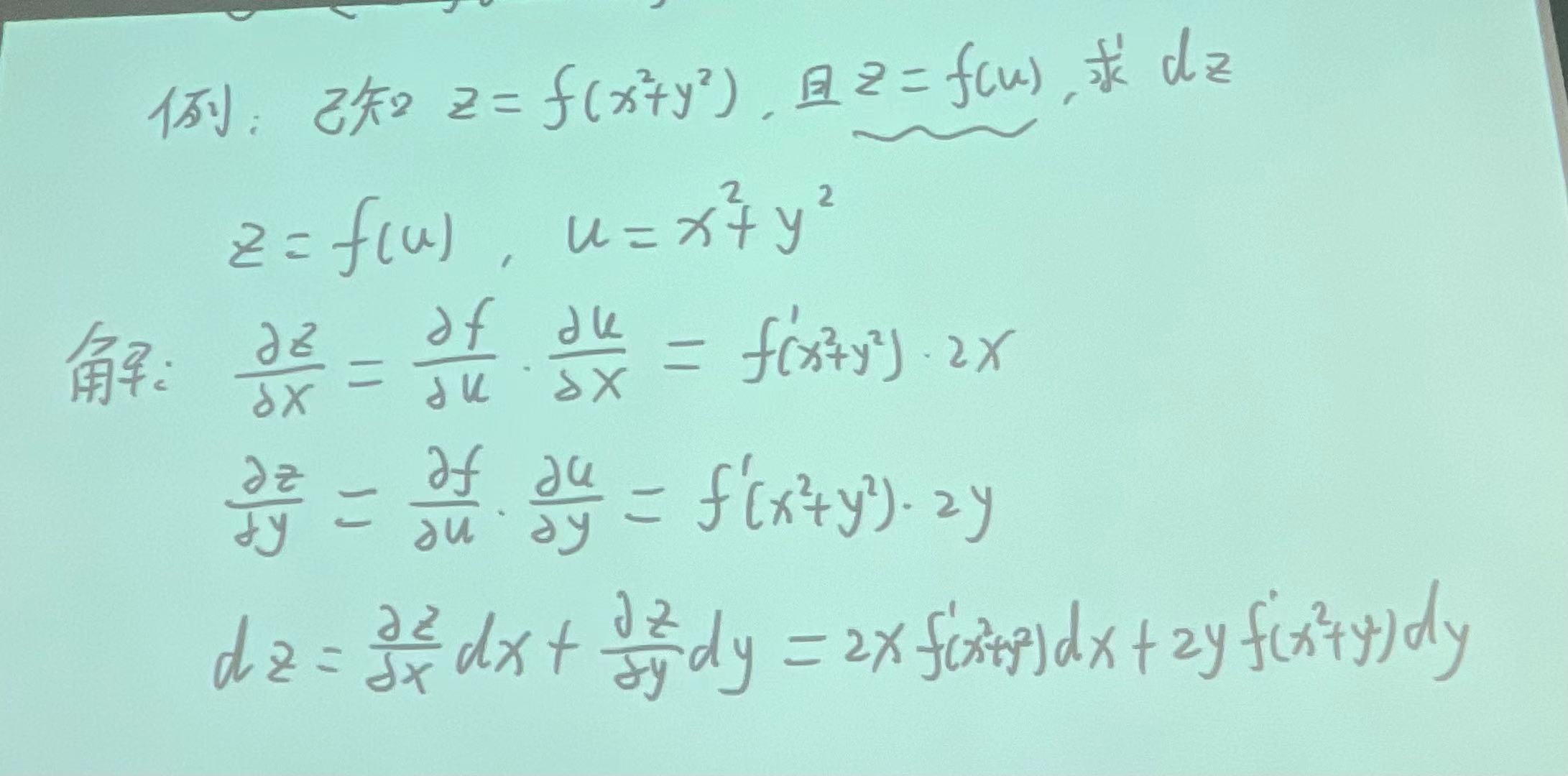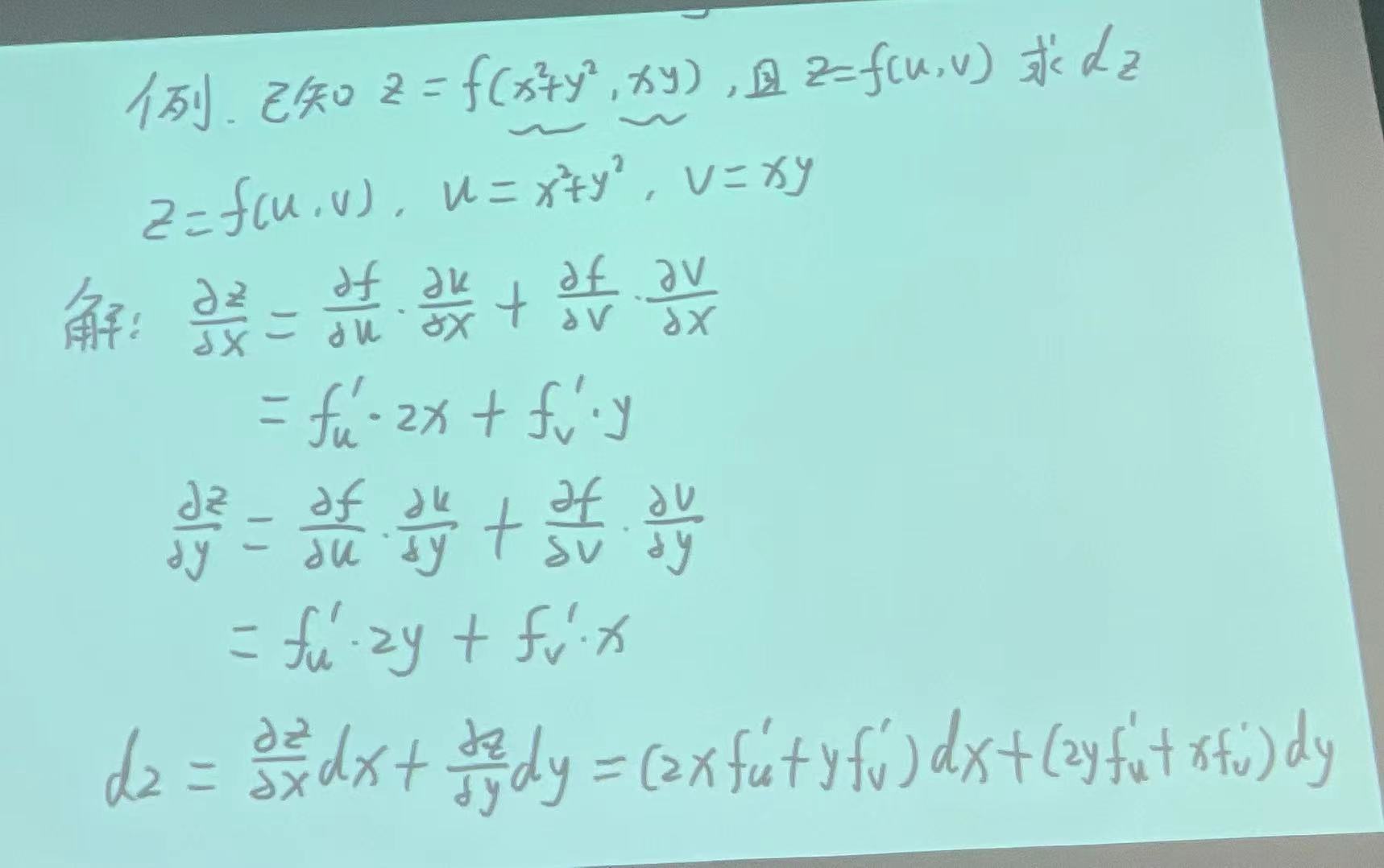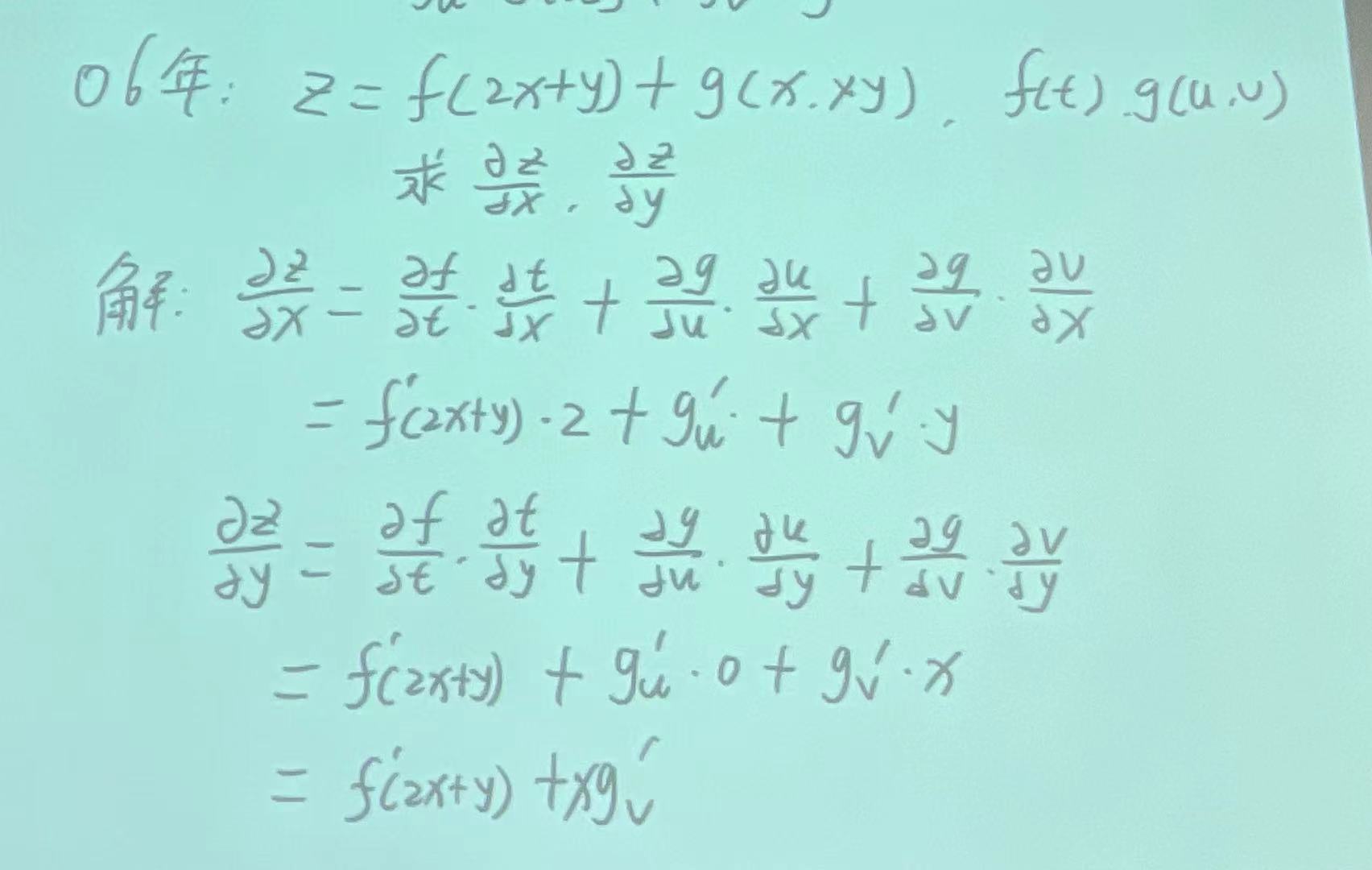二阶混合偏导：

多元函数的极值和条件极值

求条件极值时，当有约束条件且约束条件简单，可以直接转换成一元最值问题。

多元微分的几何应用

空间曲线

空间曲面

​

​

方向导数

梯度（本质是一个向量）

方向导数的最大值就是梯度的模

方向导数的最小值就是梯度的模的相反数