定积分

我的数学专升本笔记

概述

注意：

对定积分换元时，会影响积分上下限的结果，记得要将上下限的值分别代入元中的x，以求出元的上下限。

不定积分的f(x)代表的是全体原函数

定积分的f(x)代表的是一个数

变限积分的f(x)代表的是一个原函数

几何意义

变限积分

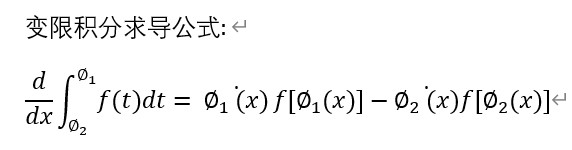
定积分的性质：

性质6的应用：

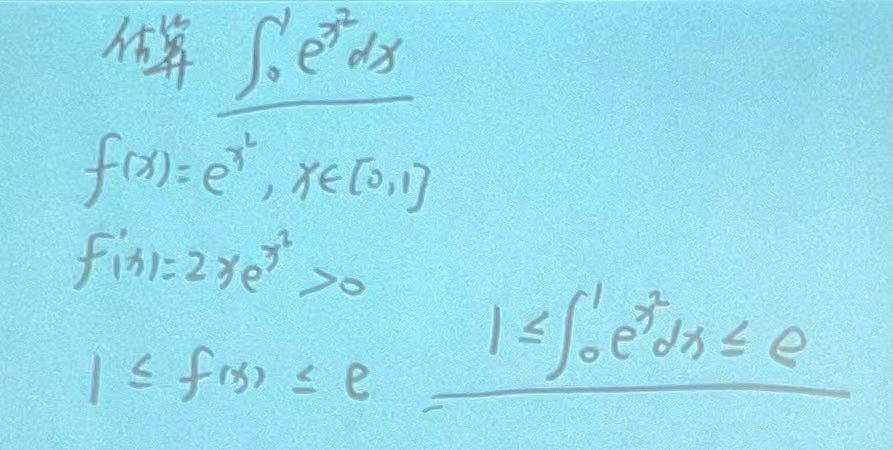
积分中值定理：

广义积分

---

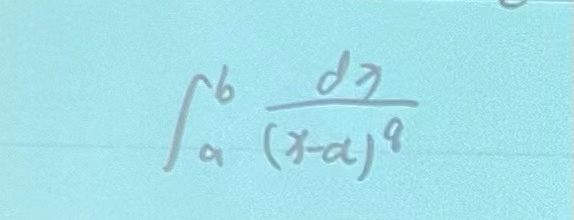1.p:分母与分子的最高次方之差；
2.积分上下限不一定是0到a，a到b适用规则也一样；
3.第一象限内，单增函数的无穷广义积分一定发散，单减函数的无穷广义积分未必收敛；
4.震荡函数的无穷广义积分一定发散；
5.否则，进行计算：能代则代，不能代单侧取极限；

可积的条件

牛顿-莱布尼茨公式

通常也被称为微积分基本定理，揭示了定积分与被积函数的原函数或者不定积分之间的联系。

特殊积分：

偶倍奇零

当被积函数有奇偶性时，直接用结论。没有奇偶性时，套公式。

结论：

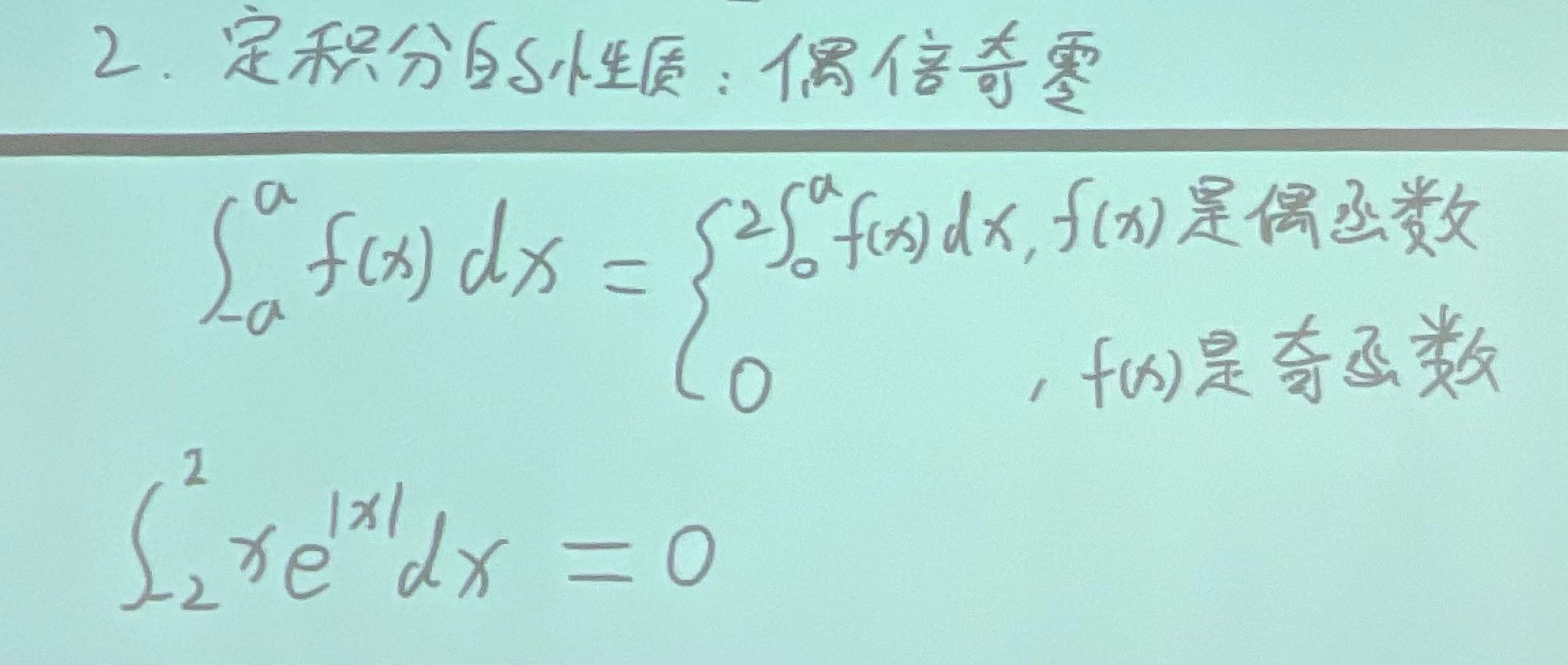
公式（适用于对称区间的定积分）：

分段函数的定积分：

1.被积函数为f(x): 分段点插入，找到对应函数再积分。
2.被积函数为f[∅(x)]: 动前不动后

case:

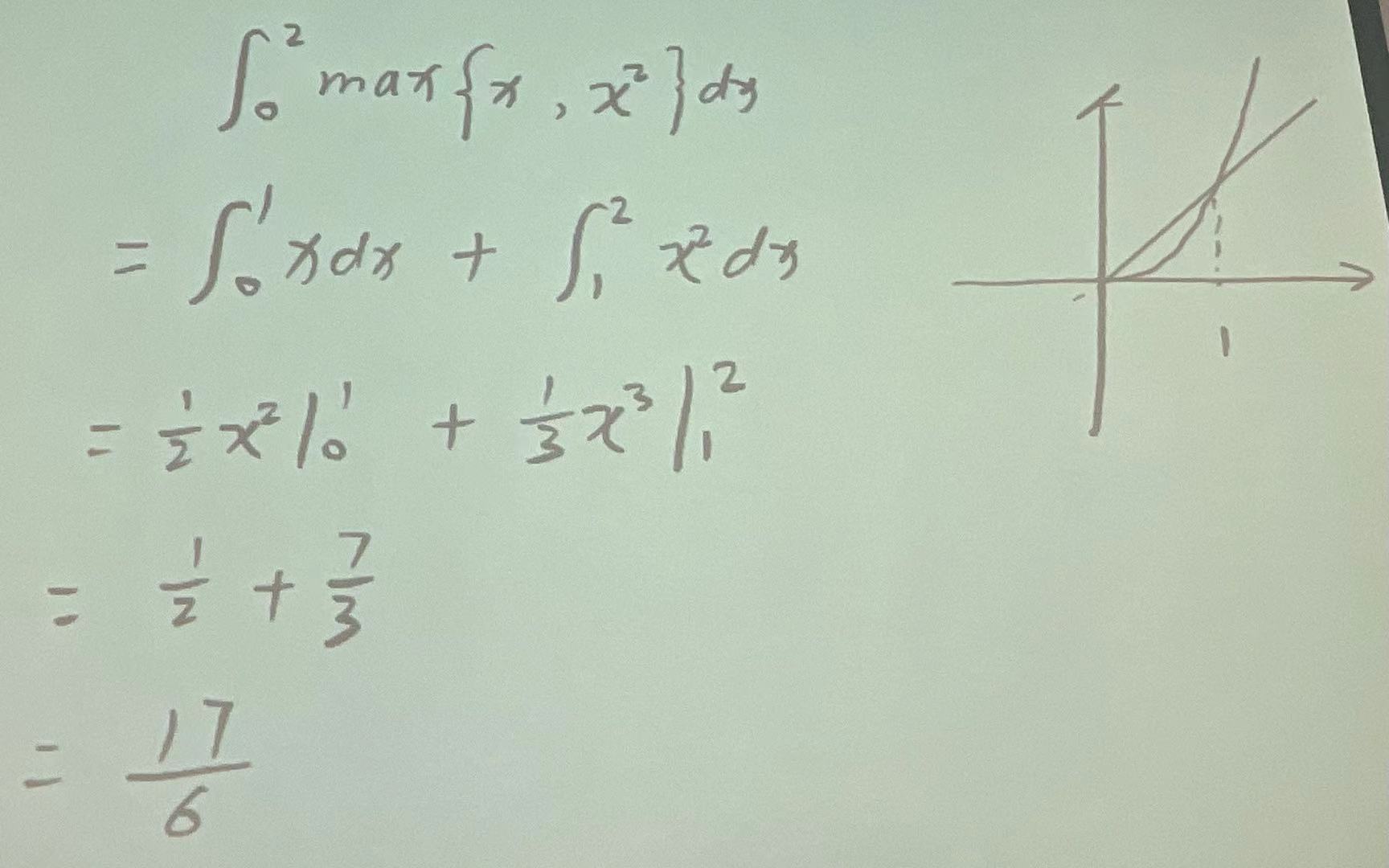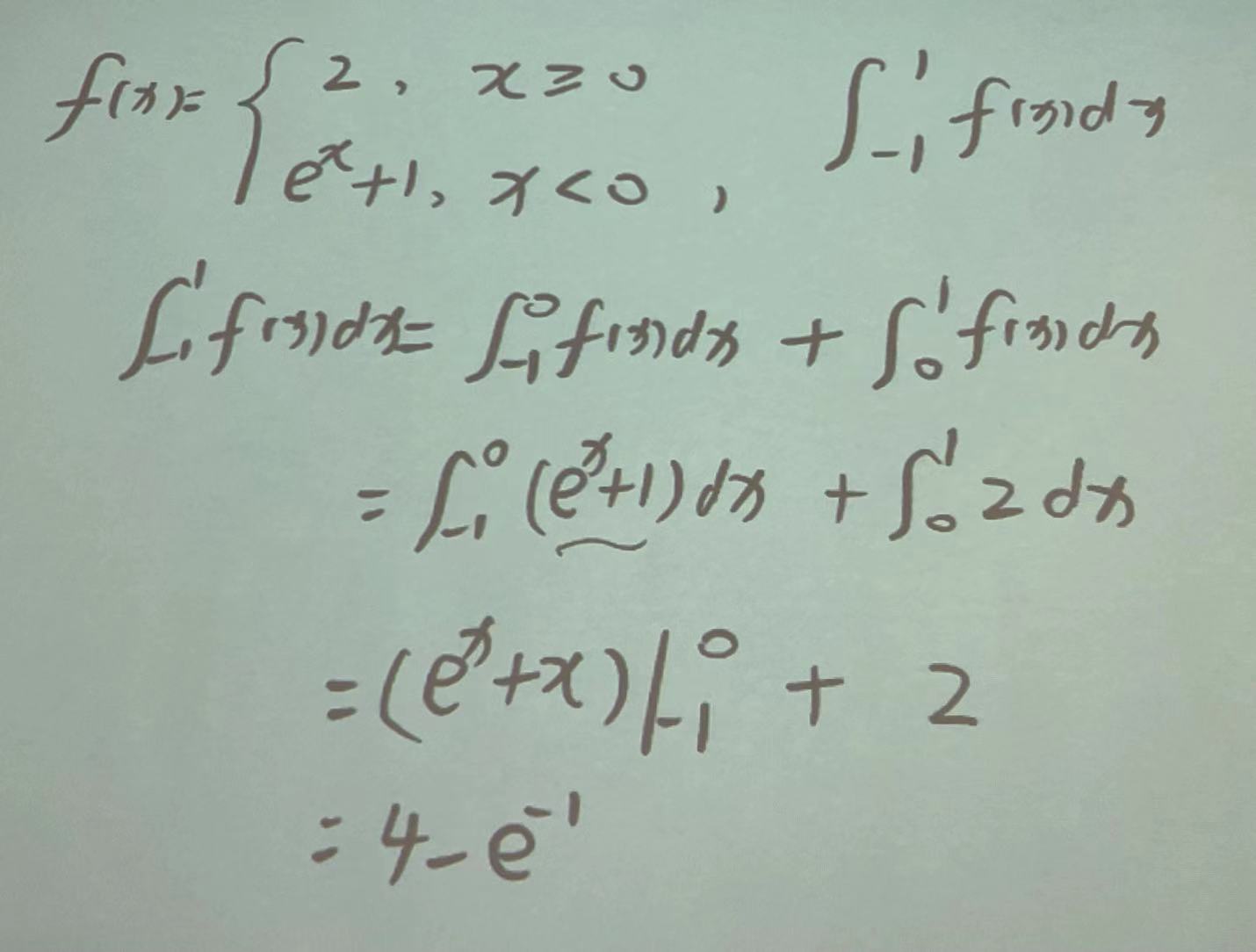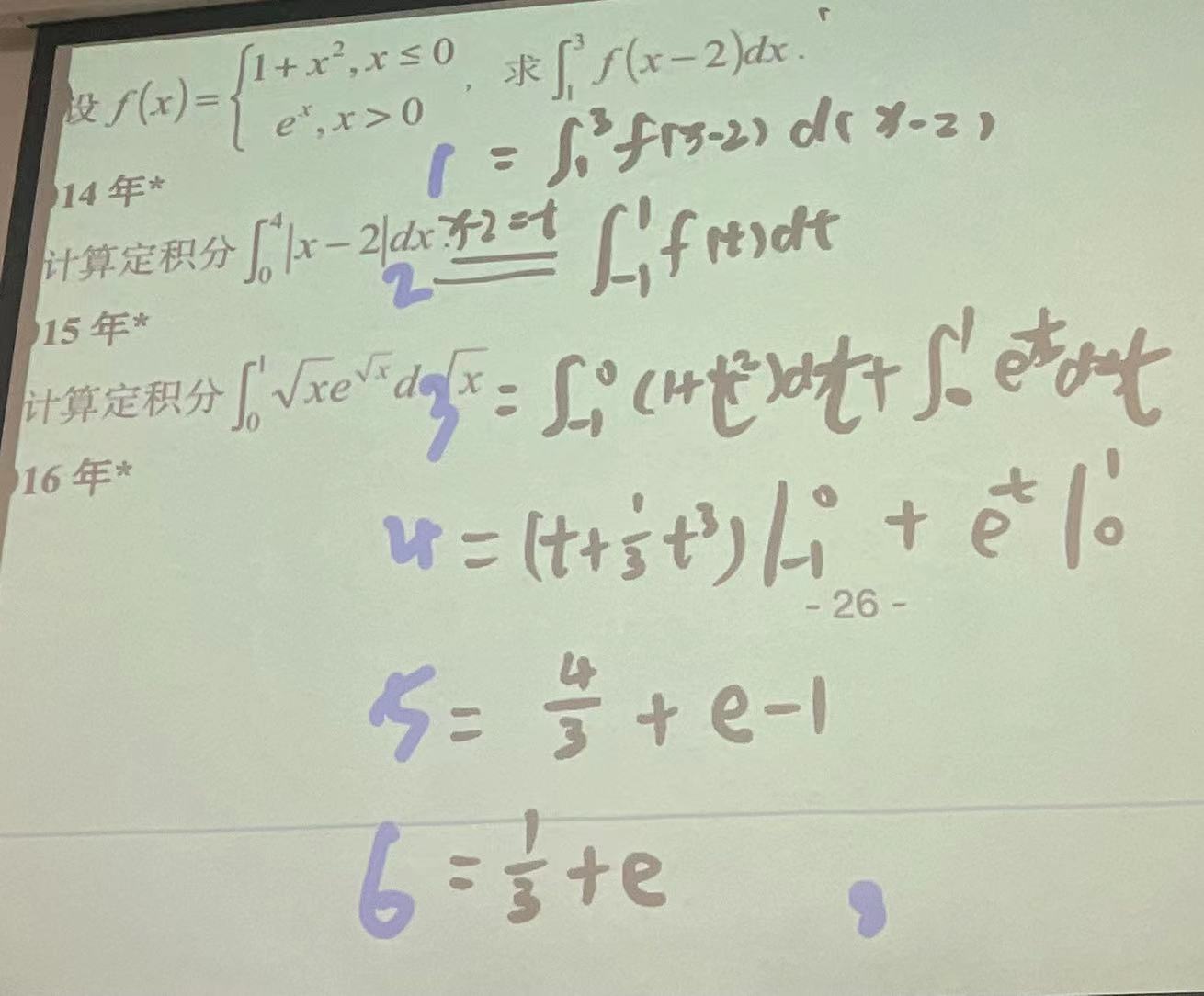华里士公式

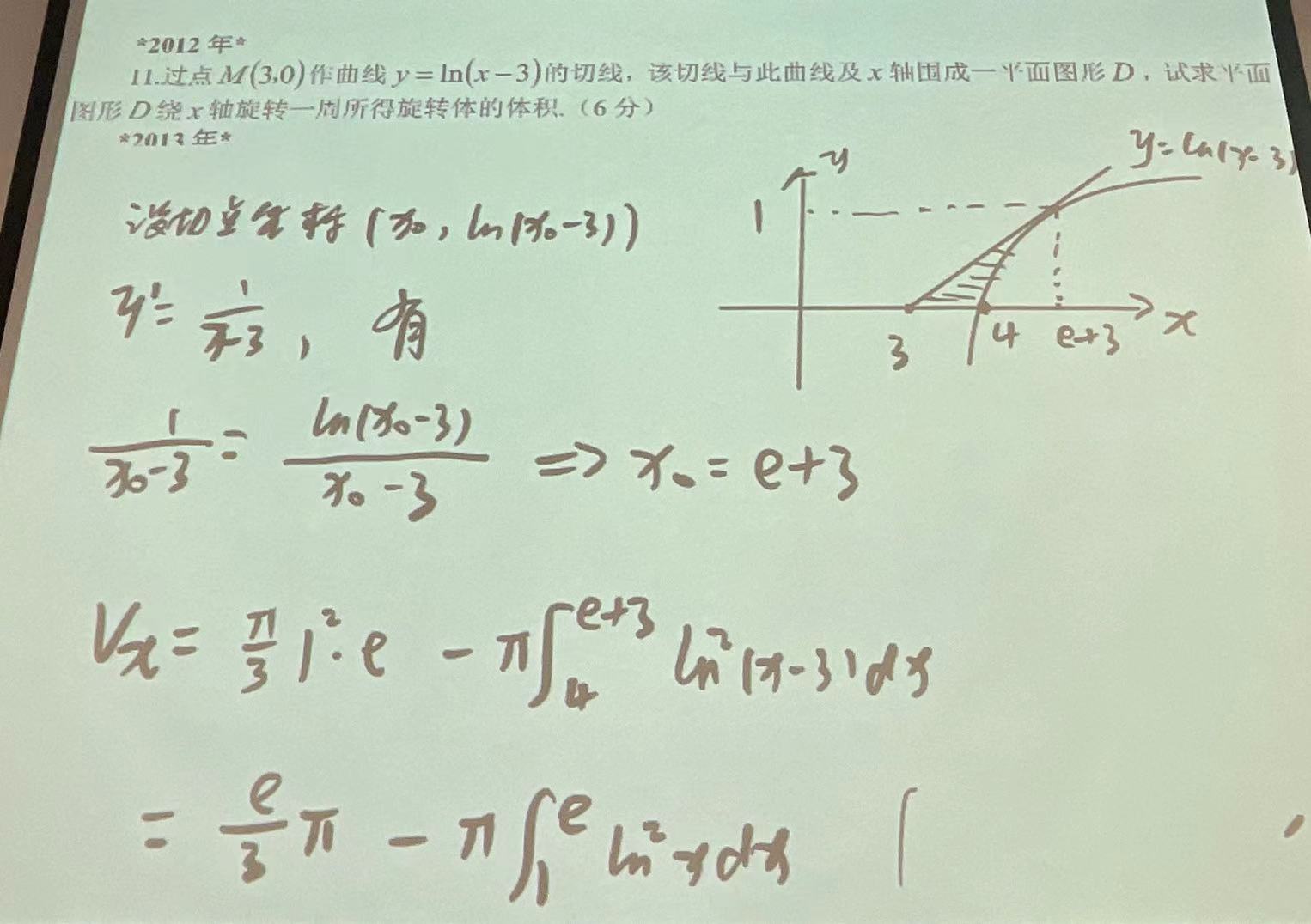
定积分的应用：

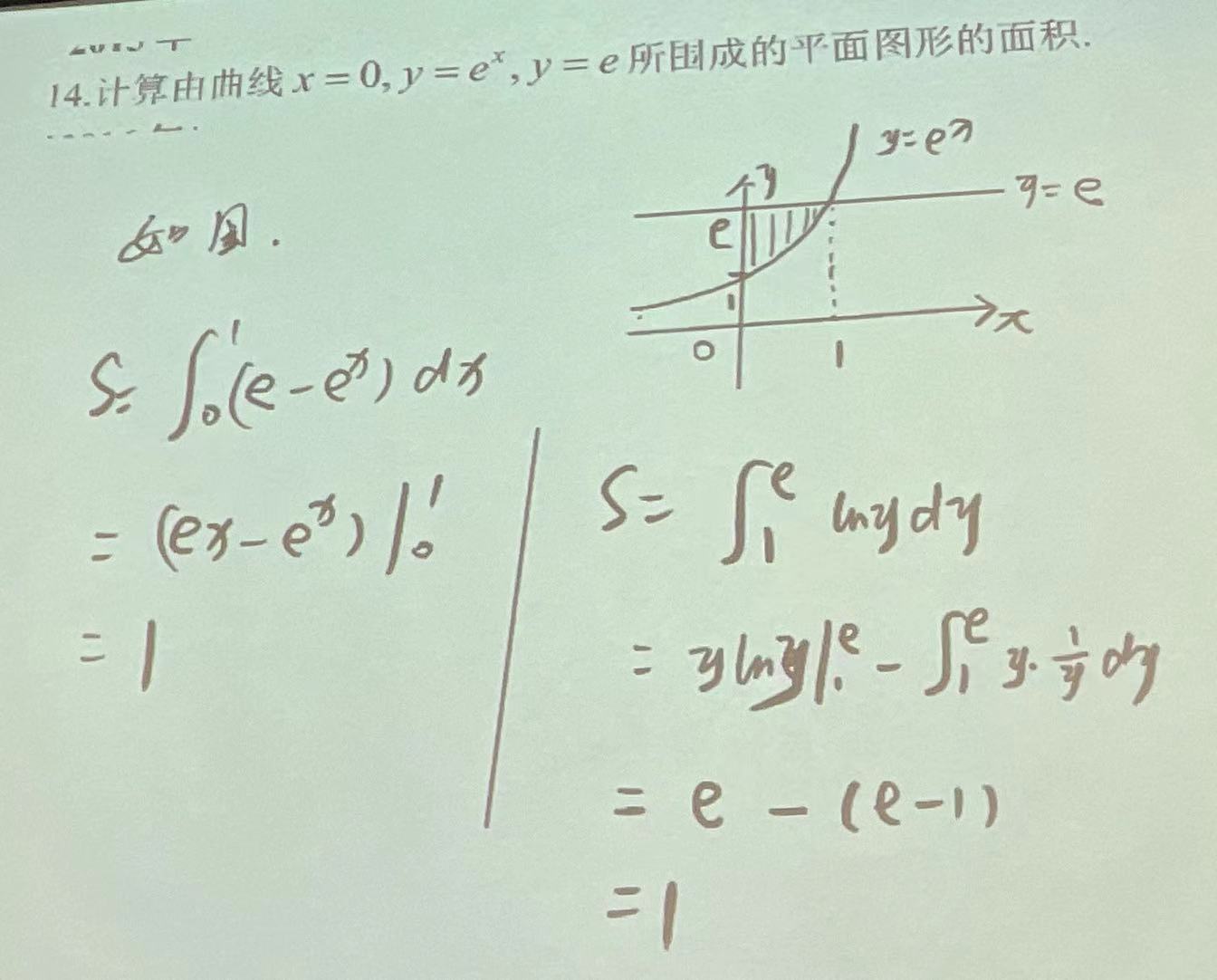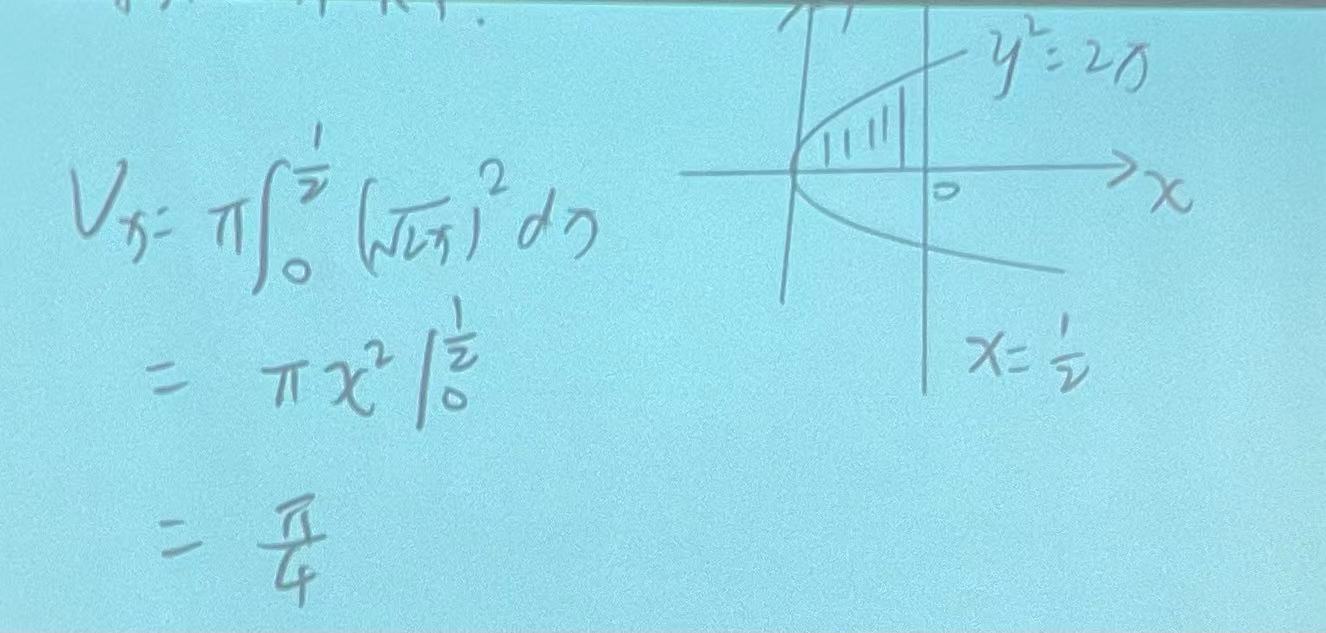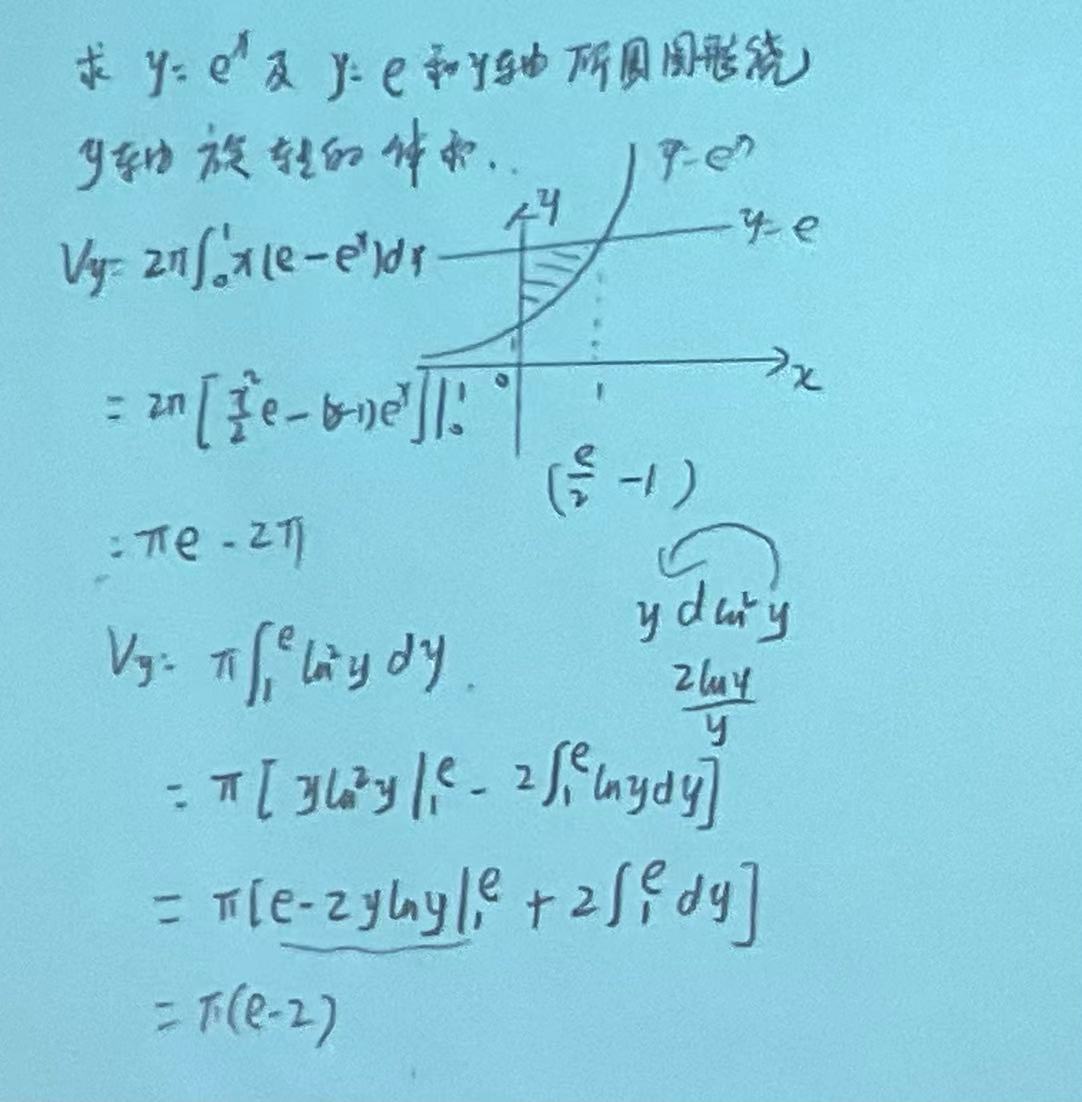一些定积分的计算：
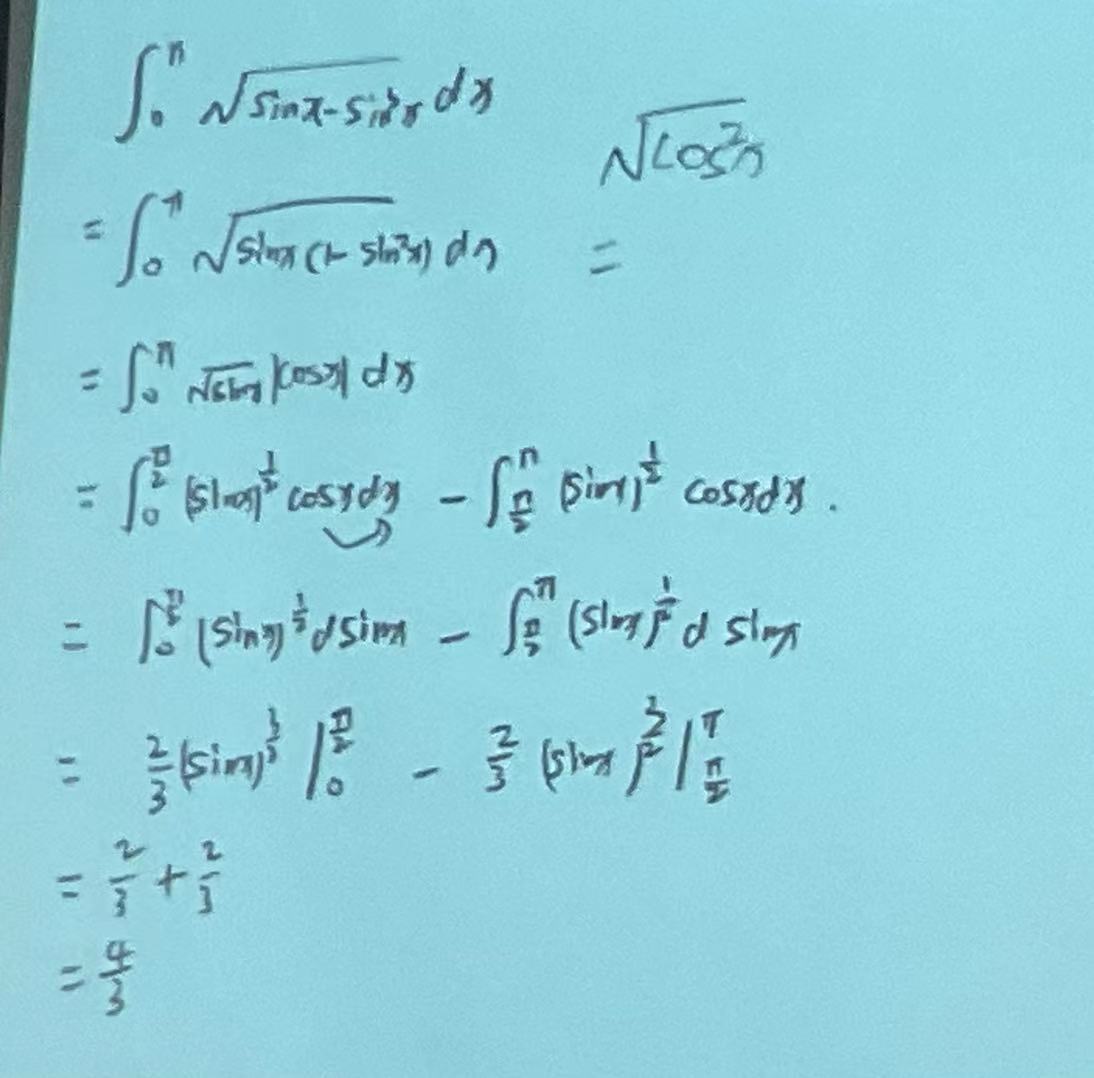
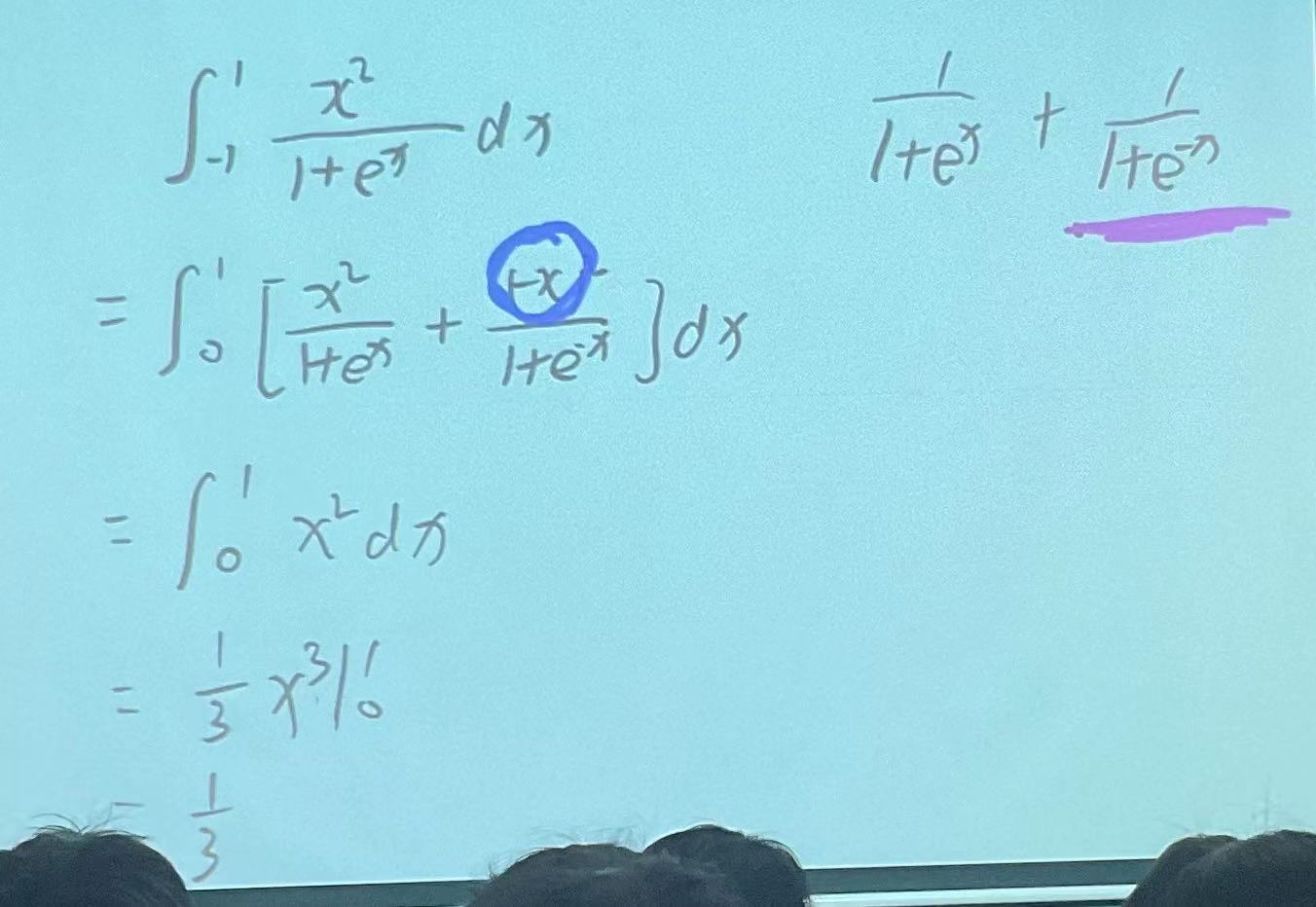