我的数学专升本笔记
基本概念:
1.可导函数的图像是一笔画成的光滑的线
2.可导的充要条件是左右导数存在且相等
3.导数的形式要求:a.分子极限 b.分母趋于0 c.上下改变量一致 d.一动一静
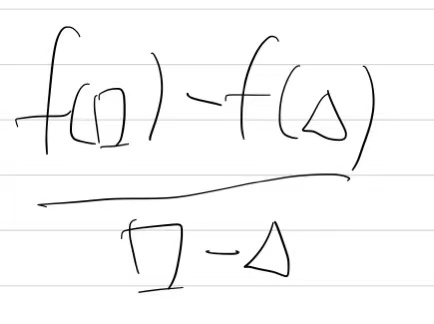
4.可导一定连续,连续不一定可导,不连续一定不可导
5.尖端(折点)不可导,(绝对值为0的点)
6.求导计算,奇偶互换
7.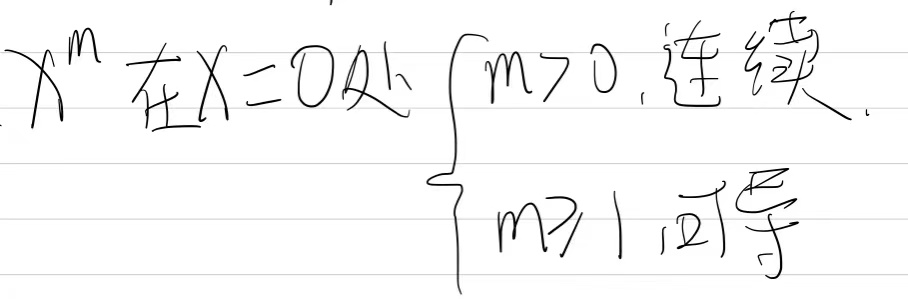
第1定义及其推论:
 |
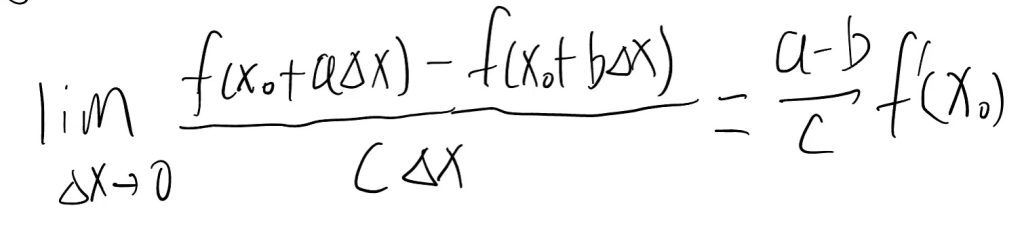 |
|---|
第2定义:
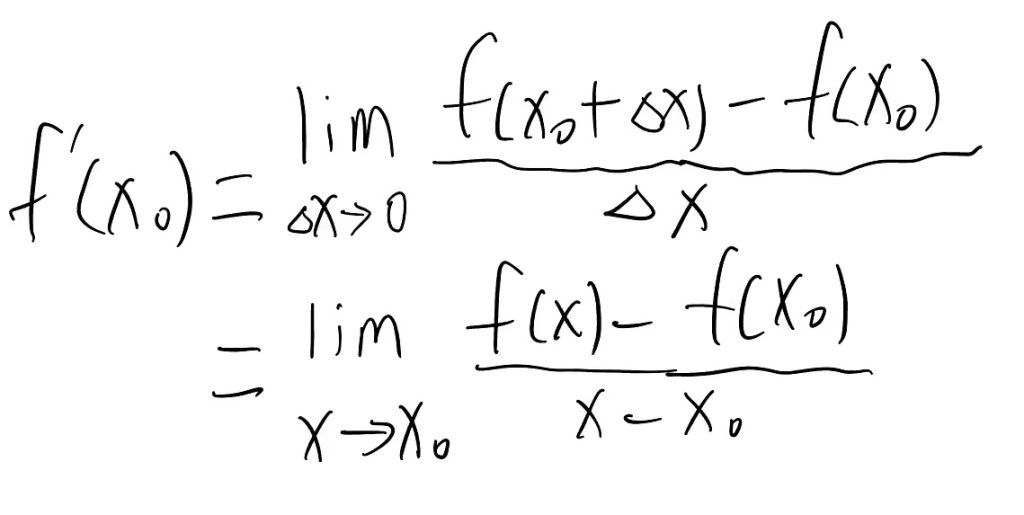
求导基本公式:
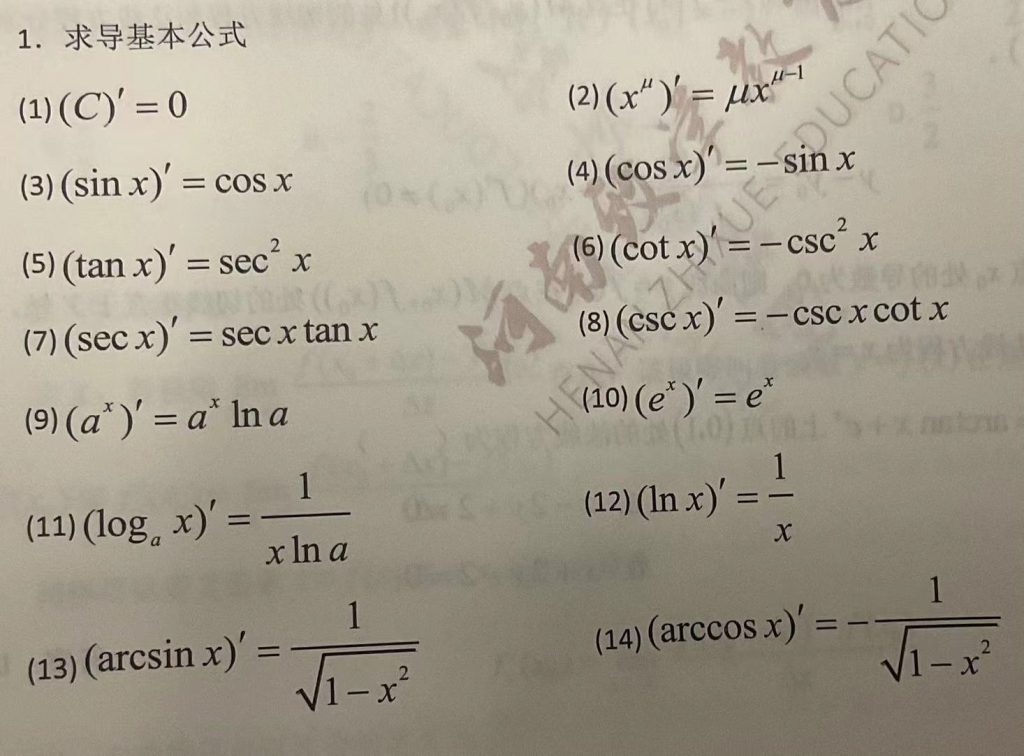 |
 |
|---|---|
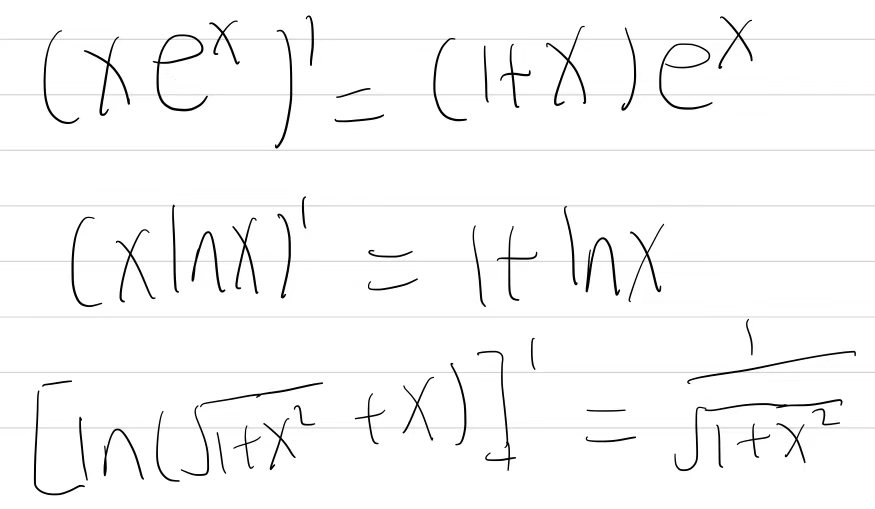 |
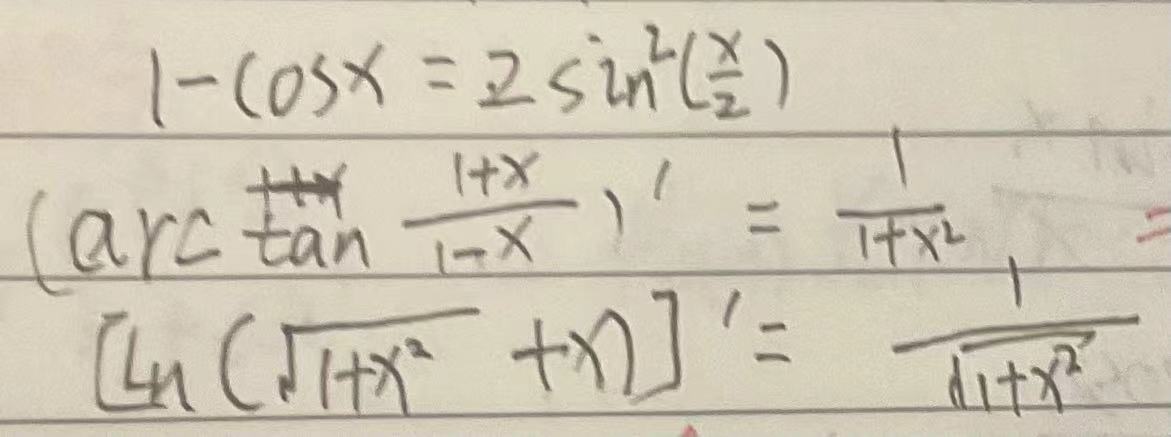 |
参数方程求导:
 |
 |
|---|---|
 |
隐函数求导:
隐函数定义:由方程F(x,y)=0所确定的函数
方法:
法一:直接求导法

法二:公式法
偏导:对谁求偏导,谁是变量,其它当作常数
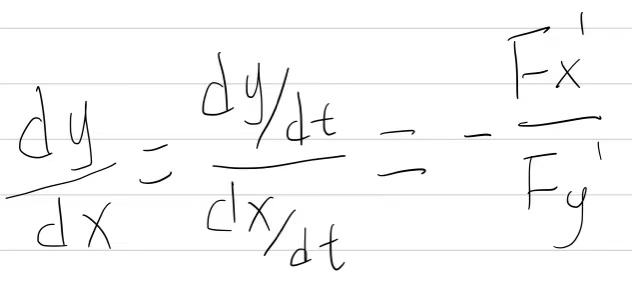 |
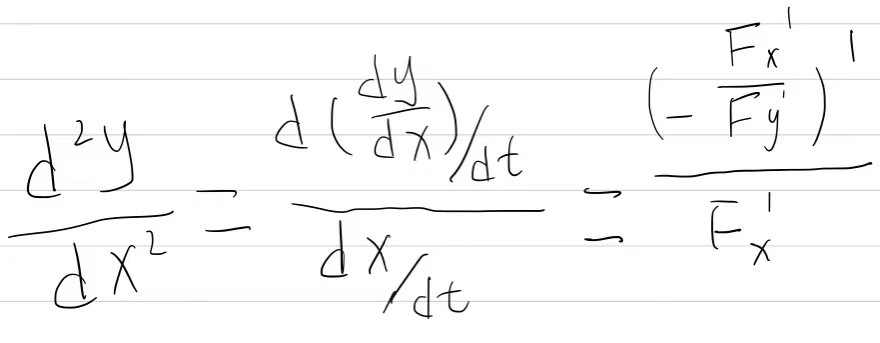 |
|---|---|
 |
对数求导法:
适用范围:1.u的v次方 2.复杂的连乘或分式

分段函数求导:
注意:看在不在分段点(分界点就是指自变量从这一点起需要带入到新的表达式进行计算的临界点.一般是一个表达式的终点以及下一个表达式的起始点,表现在图像上,可能是折点或者单独一个点或者是没有定义.)上,要注意分开讨论,如果在分断点上用导数第二定义,不在,就先找函数表达式,再求导。
高阶函数求导:
注意:找规律
高阶函数的表示:
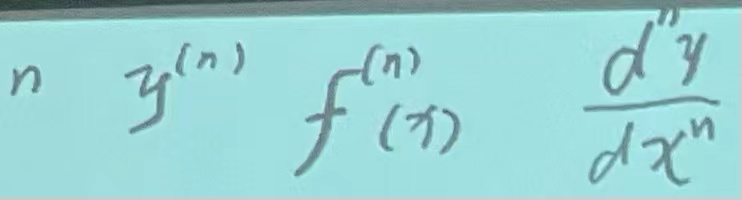 |
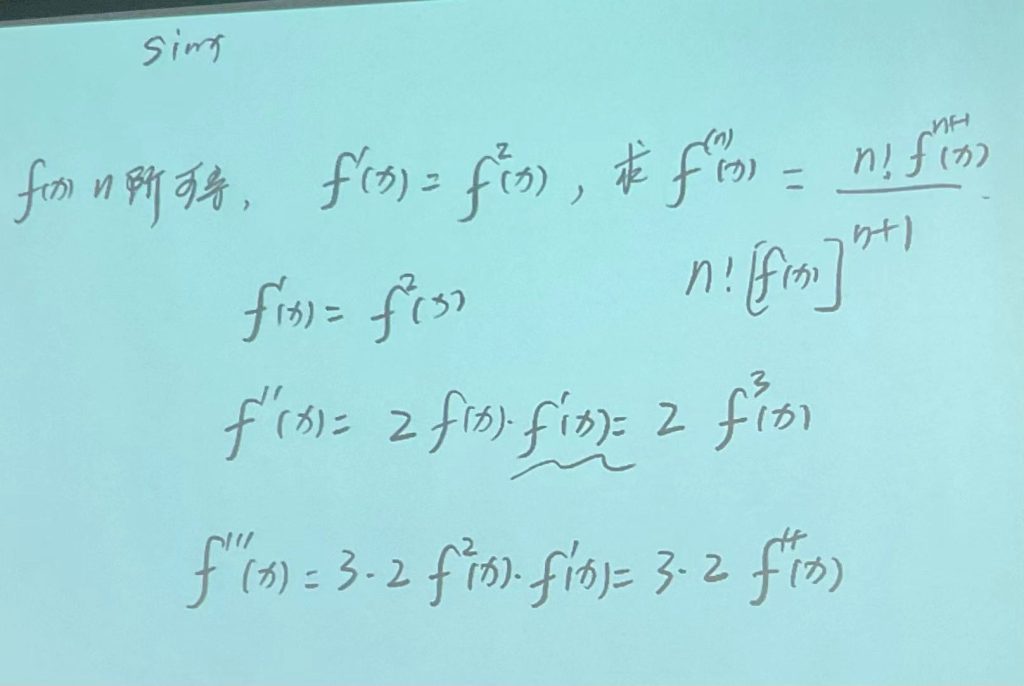 |
|---|
与切线方程结合:
 |
 |
|---|---|
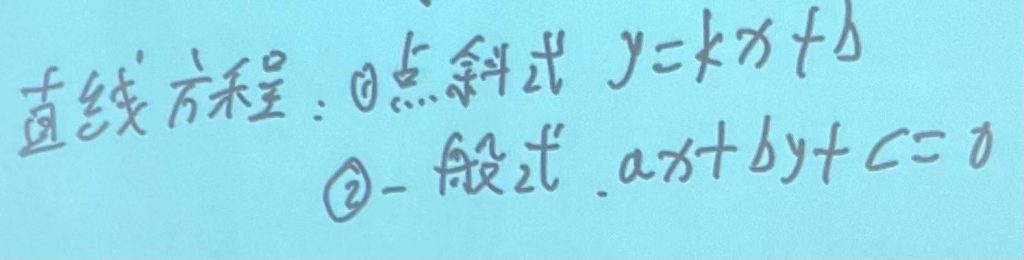 |
注意:
1.先求切点,再求斜率
2.法线:与切线垂直的线
近似值计算:

方法:(注意近似值计算只有小数,没有分数。)
 |
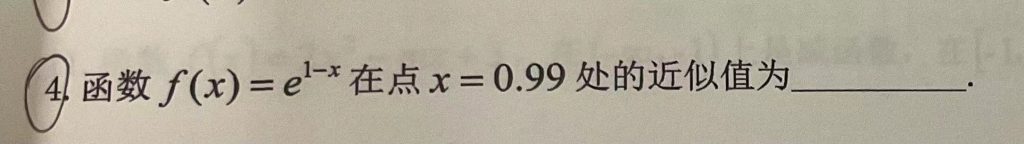 |
|---|---|
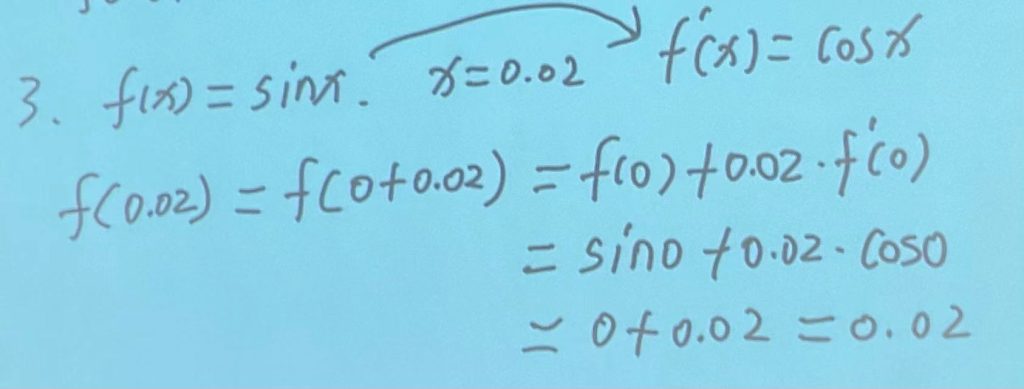 |
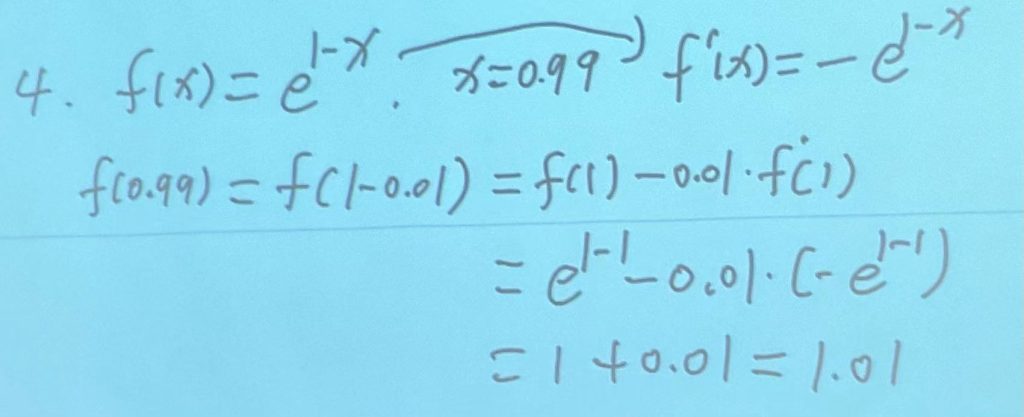 |
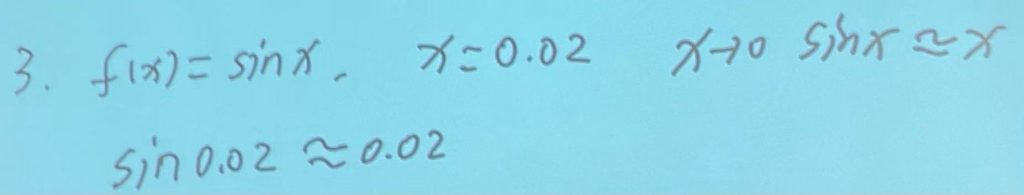 |
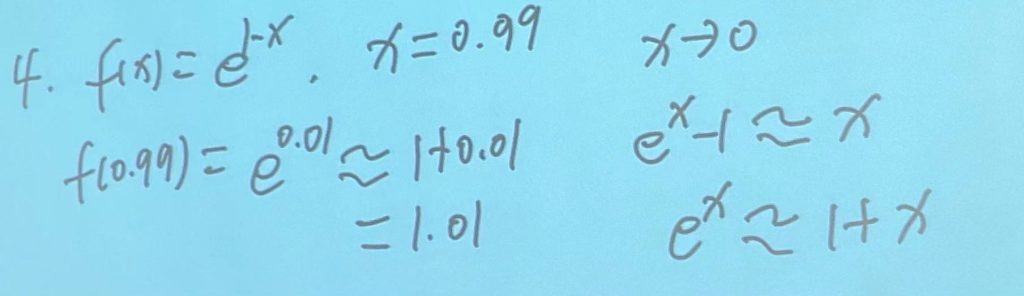 |
 |
 |
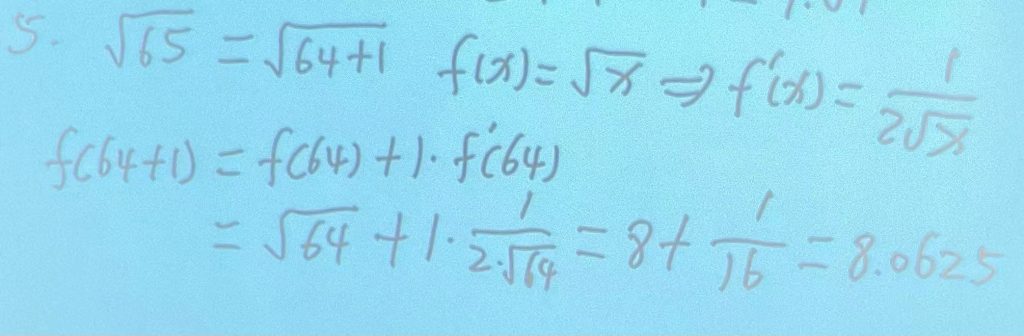 |
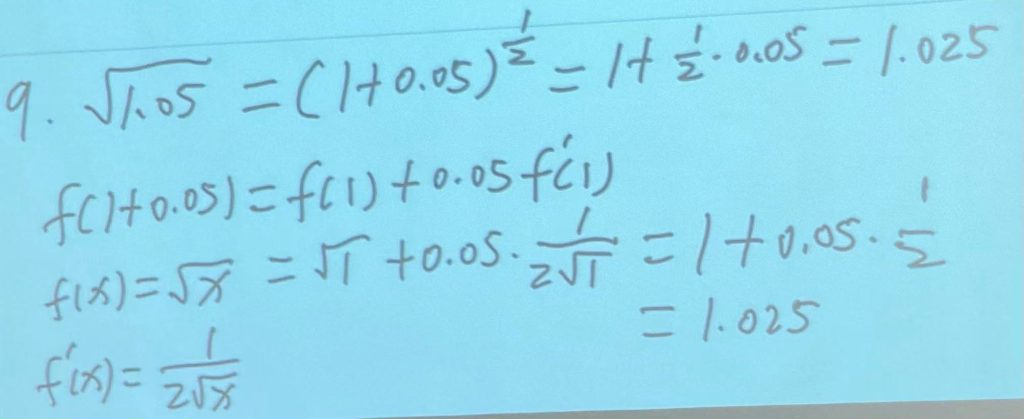 |
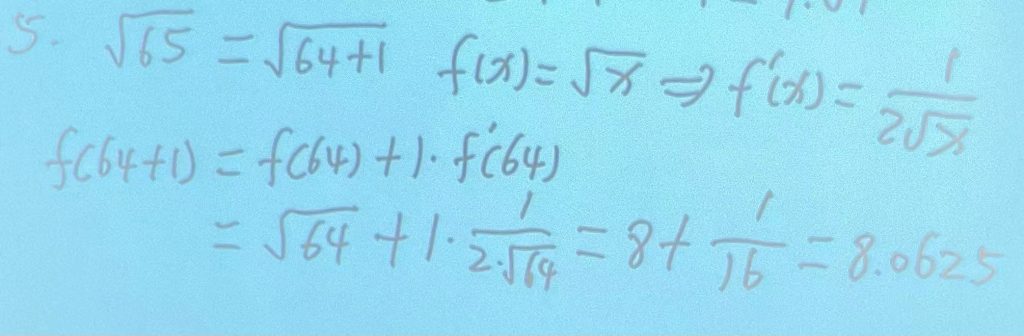 |
 |
 |
单调性,极值,最值拐点,凹凸区间和渐近线:
解题的一般步骤:
- 求函数定义域
- 求导
- 找分割点(函数等于0的点或无定义点(函数值不存在的点))
- 分点分区间去求函数的单调性和极值,求拐点时要把使函数二次导为0的点代入原函数里。
1.单调性:
函数的导数大于0,函数单调递增,函数的导数小于0,函数单调递减。
2.极值(局部概念):
 |
 |
|---|
修正:极值点驻点的第3条:二阶导存在且非零的驻点一定是极值点。
3.最值(整体概念):
解这类题要先判断函数单调性,再代入所给定义域的端点值,求出最值。
4.单调性证明不等式:
 |
 |
|---|---|
 |
 |
5.拐点和凹凸区间:
拐点:连续曲线上凹弧与凸弧的分界点。
注:1.凹凸不分先后
2.拐点是曲线上的点,写作(x0,y0),极值点是定义域内的点,写作x=x0.
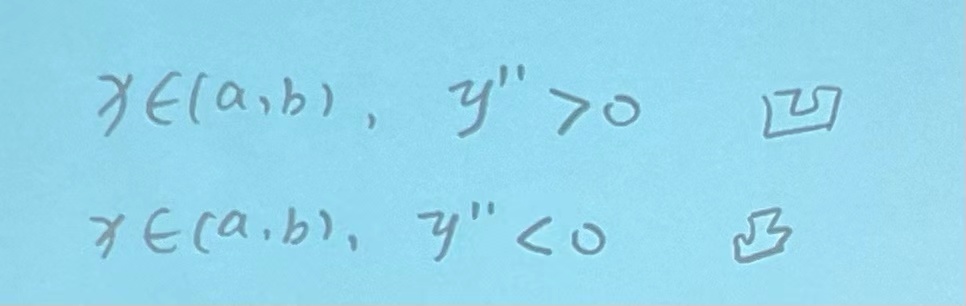
3.一切可能的拐点:1.二阶导为0的点;2.二阶导无定义的点
一切可能的极值点:1.一阶导为0的点(驻点);2.一阶导无定义的点
无意义的点:1.间断点2.取不到的端点
 |
 |
|---|
6.渐近线:

单侧趋向,水平垂直都适用
x0是f(x)的无定义点
最优化问题:

 |
 |
|---|