连续及间断

我的数学专升本笔记

基本概念：

连续函数的图像是一笔画成的线。

定义：

分段函数连续的俩种形式：

间断点及其分类：

注意：

1.间断点就是f(x)定义域以外的点

2.只有分成左右极限去求的时候，才有可能是跳跃间断点

3.可去间断点和跳跃间断点统称第一类间断点

闭区间上连续函数函数的性质：

零点定理：

罗尔定理：

对于选择题直接找条件就行，对于证明题如下（注意与零点定理比较一下区别，题目中有俩问，一般第一问考的都是零点定理）：

判断连续：

1.找函数值的定义域，若包含所给区间则连续，反之，不连续，（分段函数除外）

2.找极限值与函数值，若相等则连续。

判断可导：

1.找导数的定义域，若包含所给区间则可导，反之，不不可导，（分段函数，带绝对值的函数除外）

2.找左导和右导，若相等着可导

3.尖端不可导：使绝对值等于0的点不可导

构造辅助函数：

出题类型

还原法

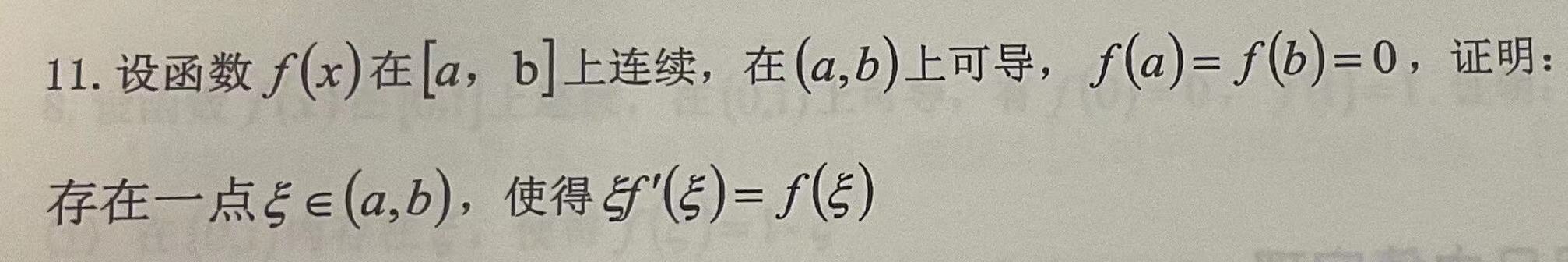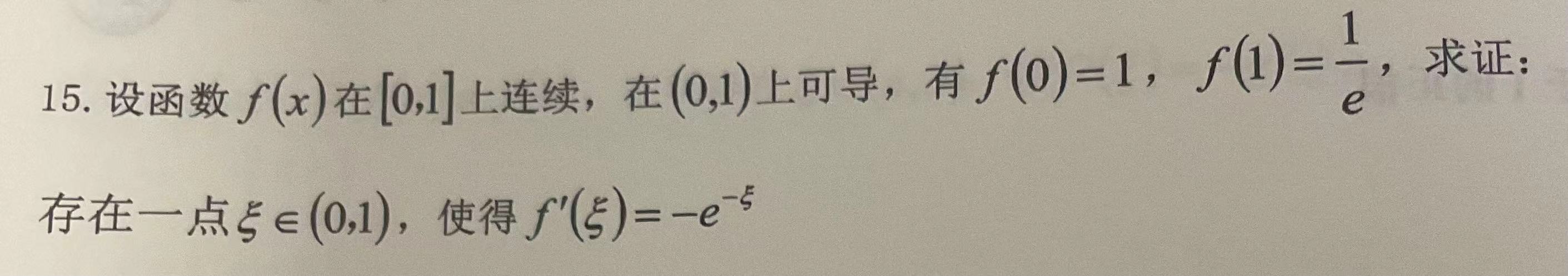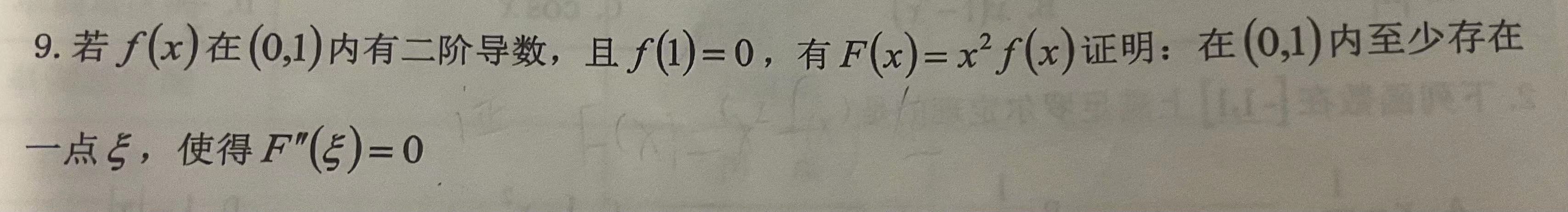拉格朗日定理：

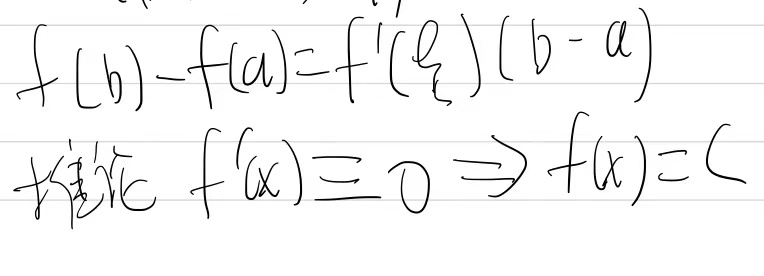适用范围：证明连体不等式（俩个及俩个以上的不等式）和含俩个不同字母的式子。

要判断原函数的单调性,就要去求其导数的正负，（正为增，负为减），要求其导数的单调性，就要找导导函数的正负。

出题类型:

中间拆开除于俩边相同的部分,定分子，换分母