极限

我的数学专升本笔记

基本概念：

1.极限存在的充要条件：左右极限存在且相等。

2.极限值是一个确定的数。

3.f（x）在X0处有极限与f（x）在X0处有定义无关。

4.计算极限时，如果能代入，代入即是极限值。

5.谁在极限符号下方谁是变量，其它当作常数。

6.

7.求极限时只有指数和arctanx区分正负无穷

无穷大量与无穷小量：

a.无穷小量和无穷大量需指明方向

b.常数中只有0在任何趋势下都是无穷小量

c.sinx和cosx是常见的有界函数，只有sin后面的未知数趋于无穷才是有界函数。

等价无穷小代换：

第一重要极限：

第二重要极限：

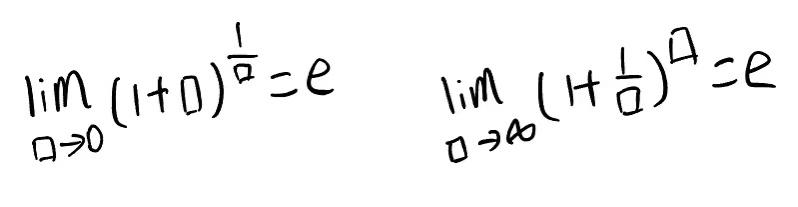
注意：该极限适用于1适用于1的无穷次方，做题时先构造e，再代公式。

做极限题的一般步骤：

求极限的方法汇总：

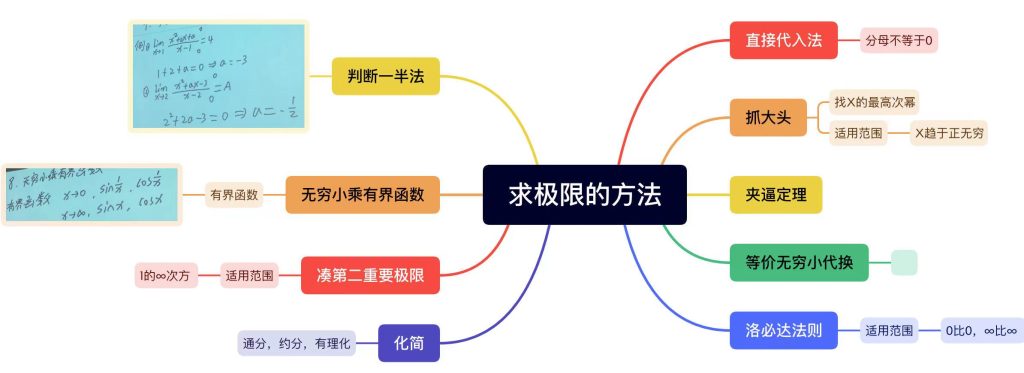
无穷小阶的比较：

注意：系数不为0，则为不等价（分子是分母的低或高阶）

极限的性质：

1.唯一性：极限存在必唯一

2.有界性：极限存在必有界，反之不对

3.收敛数列及其子列：收敛数列的子列都收敛，且极限值相同

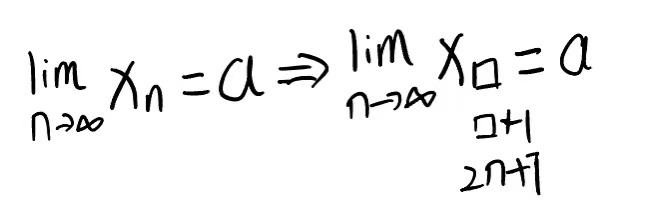
4.保号性：

5.保序性：

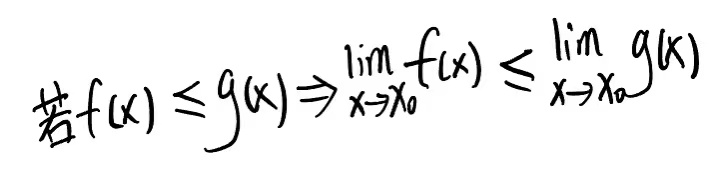
俩个收敛准则：

1.单调有界无穷函数必有极限：

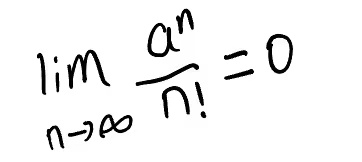
2.夹逼定理：

洛必达法则：

1.基本概念：

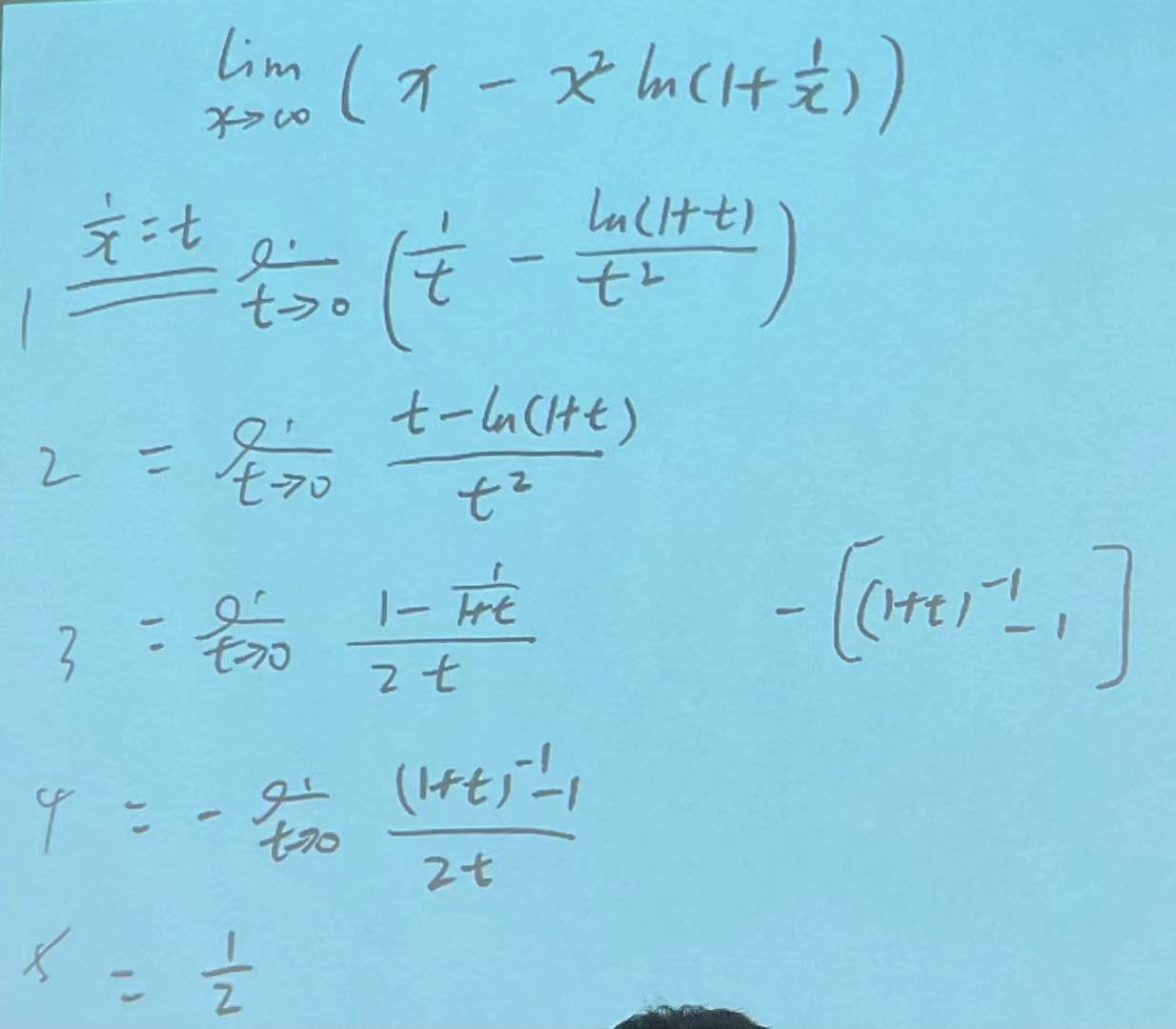2.适用范围：零比零，无穷比无穷，零比无穷（可以化为前面俩种形式）

3.求U的V次方极限：

思路：

a.指数化（这时注意指数化之后，简单的做分母）

b.用洛必达

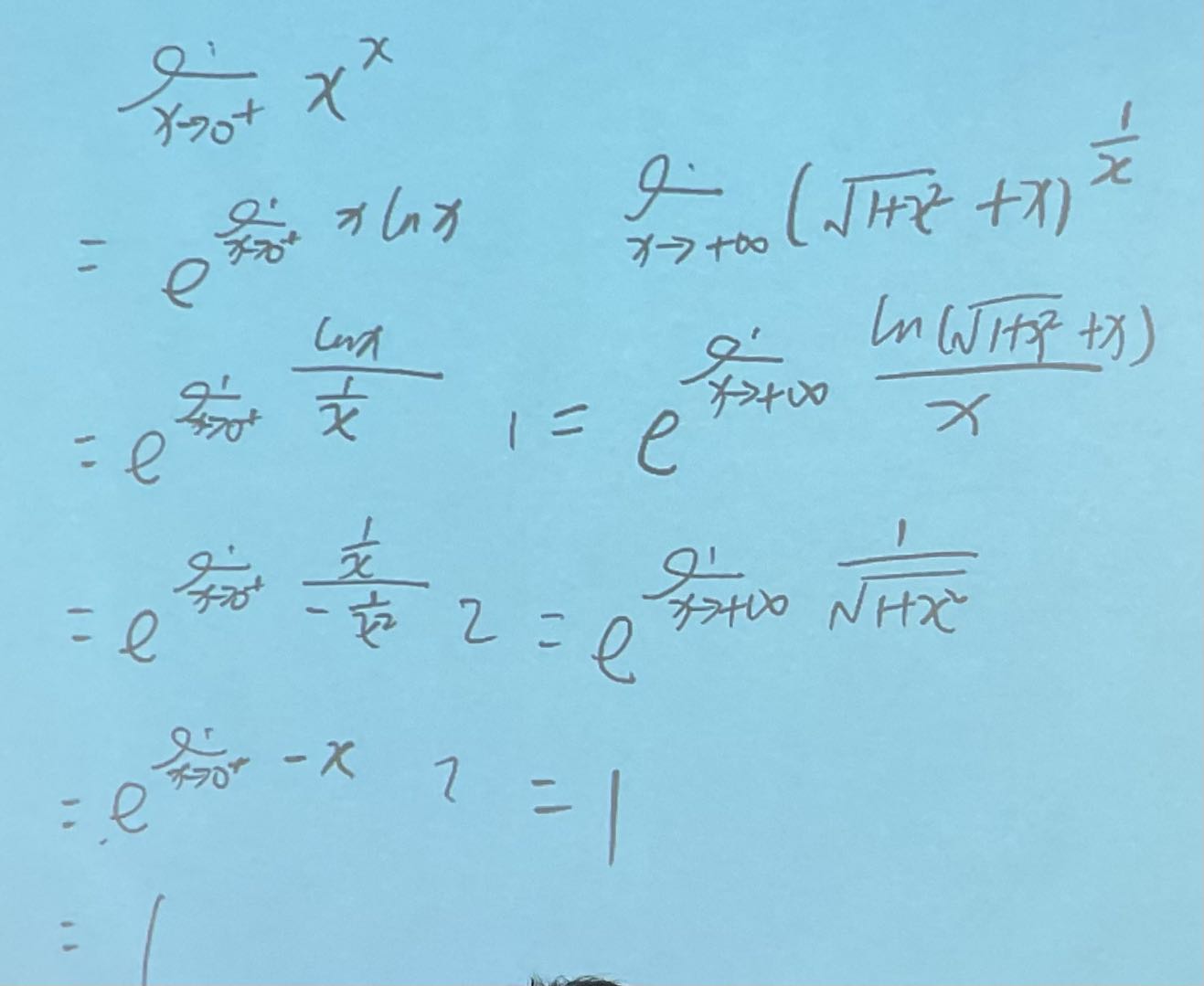
4.变限积分（一定使用洛必达）
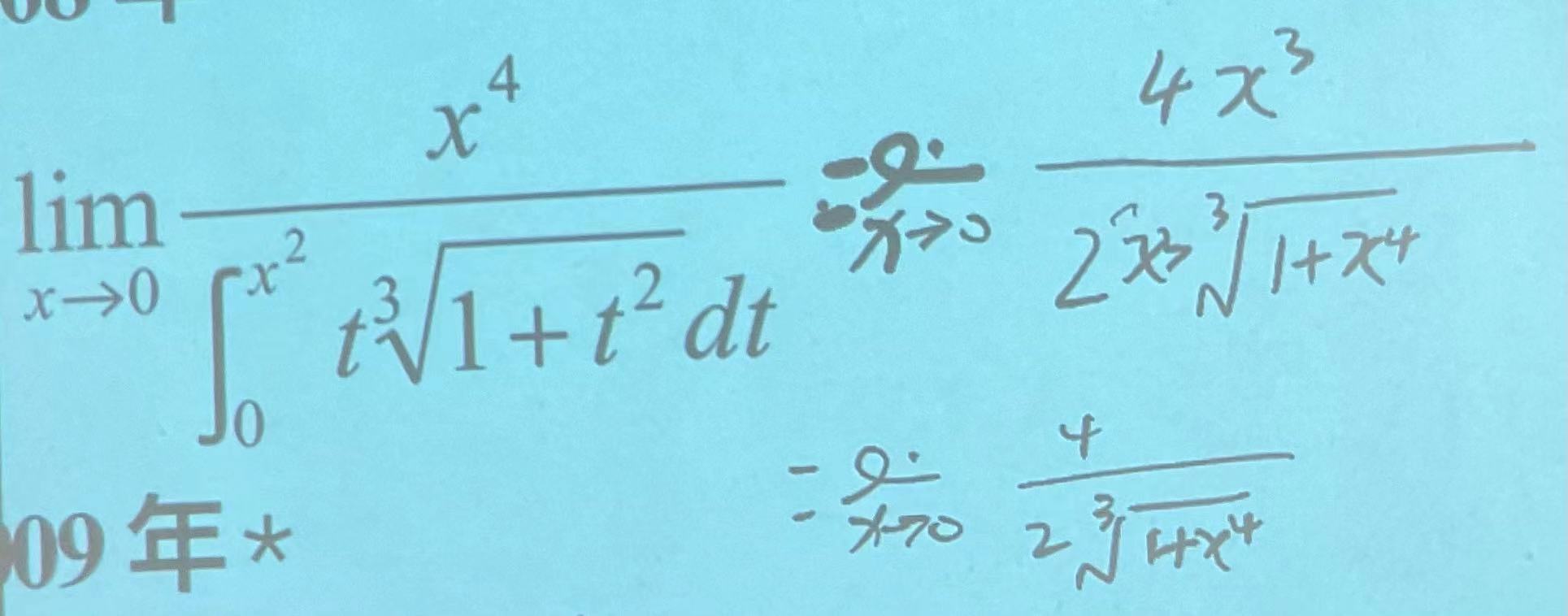